
分析 利用利用三角形的面積公式推出x+y+z=$\sqrt{3}$,結合條件,根據x+y+z≥3•$\root{3}{xyz}$,當且僅當x=y=z時,等號成立,推出x=y=z即可解決問題.
解答 解:∵△ABC是等邊三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$•22=$\sqrt{3}$=$\frac{1}{2}$•2•(x+y+z),
∵x+y+z=$\sqrt{3}$,
∵xyz=$\frac{\sqrt{3}}{9}$,
又∵x+y+z≥3•$\root{3}{xyz}$,當且僅當x=y=z時,等號成立,
∵x+y+z=$\sqrt{3}$,3•$\root{3}{xyz}$=3•$\root{3}{\frac{\sqrt{3}}{9}}$=$\root{3}{27×\frac{\sqrt{3}}{9}}$=$\root{3}{3\sqrt{3}}$=$\root{3}{(\sqrt{3})^{3}}$=$\sqrt{3}$,
∴x+y+z=3•$\root{3}{xyz}$,
∴x=y=z=$\frac{\sqrt{3}}{3}$,
∴x2+y2+z2=$\frac{1}{3}$+$\frac{1}{3}$+$\frac{1}{3}$=1.
故答案為1.
點評 本題考查三角形綜合題、等邊三角形的性質,解題的關鍵是用到不等式:x+y+z≥3•$\root{3}{xyz}$,當且僅當x=y=z時,等號成立,只要證明等號成立,即可解決問題,屬于競賽題目.


科目:初中數學 來源: 題型:選擇題
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
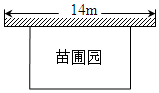 某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊周長為30米的籬笆圍成.已知墻長為14米(如圖所示),設這個苗圃園垂直于墻的一邊長為x米.
某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊周長為30米的籬笆圍成.已知墻長為14米(如圖所示),設這個苗圃園垂直于墻的一邊長為x米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
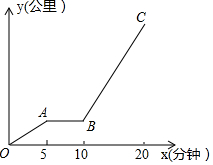 李狗蛋從家出發坐公交車去上學,他要先走到公交車站等公交車.他離家的距離y(米)與經過的時間x(分鐘)的關系折線如圖所示,已知狗蛋每分鐘能走0.1公里,公交車的速度為0.4公里/分鐘.
李狗蛋從家出發坐公交車去上學,他要先走到公交車站等公交車.他離家的距離y(米)與經過的時間x(分鐘)的關系折線如圖所示,已知狗蛋每分鐘能走0.1公里,公交車的速度為0.4公里/分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4 | 3 | 2 | 1 | 0 | … |
| A. | y=-2x | B. | y=x+4 | C. | y=-x+2 | D. | y=2x-2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com