

分析 (1)只要證明△ACD≌△BCE,A、B、H、C四點共圓,即可解決問題.
(2)(3)(4)方法類似(1).
解答 解:(1)如圖1中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,α=60°,
∴△ABC,△CDE都是等邊三角形,
∴∠BAC=∠ACB=60°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ADC=∠BDH,
∴∠BHD=∠ACD=60°,
∴∠AHE=120°,A、B、H、C四點共圓,
∴∠BHC=180°-∠BAC=120°.
(2)如圖2中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,α=90°,
∴△ABC,△CDE都是等腰直角三角形,∠ACD=∠BCE,
∴∠BAC=∠ABC=45°,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、B、H、C四點共圓,
∴∠BHA=∠ACB=90°,∠BHC=180°-∠BAC=135°
∴∠AHE=180°-∠BHA=90°.
(3)如圖3中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∠ACD=∠BCE,
∴∠BAC=90°-$\frac{1}{2}$α,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、B、H、C四點共圓,
∴∠BHA=∠ACB=α,
∴∠AHE=∠ACB=α,∠BHC=180°-∠BAC=90°+$\frac{1}{2}$α.
(4)如圖4中,
∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∠ACD=∠BCE,
∴∠BAC=90°-$\frac{1}{2}$α,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∴A、H、B、C四點共圓,
∴∠AHE=180°-∠ACB=180°-α,∠BHC=∠BAC=90°-$\frac{1}{2}$α.
點評 本題考查全等三角形的判定和性質、四點共圓等知識,解題的關鍵是四點共圓的判定和性質,難點是用到四點共圓的判定.


科目:初中數學 來源: 題型:選擇題
| A. | $\frac{10}{x}$=$\frac{3}{40}$ | B. | $\frac{10}{x}$=$\frac{1}{40}$ | C. | $\frac{10}{x}$=$\frac{1}{3}$ | D. | $\frac{10}{x+10}$=$\frac{3}{40}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB是⊙O的直徑,弦CD⊥AB于點M,連結CO,CB.
如圖,AB是⊙O的直徑,弦CD⊥AB于點M,連結CO,CB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 月使用費(元) | 主叫限定時間(分鐘) | 主叫超時費/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免費 |
| 方式二 | 88 | 350 | 0.19 | 免費 |
| A. | 方式一 | B. | 方式二 | C. | 兩種方式一樣 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
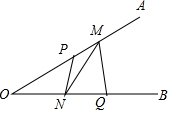 已知∠AOB=30°,點P、Q分別是邊OA、OB上的定點,OP=3,OQ=4,點M、N是分別是邊OA、OB上的動點,則折線P-N-M-Q長度的最小值是5.
已知∠AOB=30°,點P、Q分別是邊OA、OB上的定點,OP=3,OQ=4,點M、N是分別是邊OA、OB上的動點,則折線P-N-M-Q長度的最小值是5.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com