
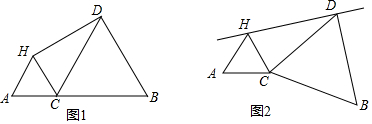
分析 (1)根據△HAC與△DCB都是等邊三角形,可得∠ACH=∠DCB=60°,AC=HC,BC=CD,進而得出∠HDC=180°-∠DHC-∠HCD=30°,得出CD=2CH,即可得到BC=2AC,最后求得$\frac{BC}{AC}$的值;
(2)先由對稱性得∠EHD=90°,EH=HC,根據E,H,C三點共線,以及三角形外角性質,得出∠AEC=$\frac{1}{2}$∠AHC=30°,由(1)可得BC=2CH=EC,得出∠BEC=$\frac{1}{2}$∠ACE=30°,即可得出CE平分∠AEB;
(3)由對稱性可知:HC=HE,進而得出A,C,E都在以H為圓心,HA為半徑的圓上,據此得到∠AEC=$\frac{1}{2}$∠AHC=30°,而同理可得,∠BEC=$\frac{1}{2}$∠BDC=30°,最后得出EC平分∠AEB.
解答 解:(1)∵△HAC與△DCB都是等邊三角形,
∴∠ACH=∠DCB=60°,AC=HC,BC=CD,
∴∠HCD=180°-∠ACH-∠DCB=60°,
∵∠DHC=90°,
∴∠HDC=180°-∠DHC-∠HCD=30°,
∴CD=2CH,
∴BC=2AC,
∴$\frac{BC}{AC}$=2;
(2)如圖1,由對稱性得∠EHD=90°,EH=HC,
∵AH=HC,
∴EH=AH,
∵∠DHC=90°,
∴E,H,C三點共線,
∴∠AEC=$\frac{1}{2}$∠AHC=30°,
由(1)可得BC=2CH=EC,
∴∠BEC=$\frac{1}{2}$∠ACE=30°,
∴∠AEC=∠BEC,即CE平分∠AEB;
(3)結論仍然正確,理由如下:
如圖2,由對稱性可知:HC=HE,
又∵AH=HC,
∴HC=HA=HE,
∵A,C,E都在以H為圓心,HA為半徑的圓上,
∴∠AEC=$\frac{1}{2}$∠AHC=30°,
同理可得,∠BEC=$\frac{1}{2}$∠BDC=30°,
∴∠AEC=∠BEC,
∴EC平分∠AEB.
點評 本題屬于三角形綜合題,主要考查了等邊三角形的性質,圓周角定理以及軸對稱的性質的綜合應用,解題時注意:如果兩個圖形關于某直線對稱,那么對稱軸是任何一對對應點所連線段的垂直平分線;解題的關鍵是運用等邊三角形的三個內角都相等,且都等于60°.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知反比例函數y1=$\frac{k_1}{x}$與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.
如圖,已知反比例函數y1=$\frac{k_1}{x}$與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
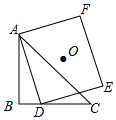 如圖,△ABC中,∠ABC=90°,AB=BC=4,D為BC邊上一動點,點O是正方形ADEF的中心,當點D沿BC邊從點B運動到點C時,點O運動的路徑長為2$\sqrt{2}$.
如圖,△ABC中,∠ABC=90°,AB=BC=4,D為BC邊上一動點,點O是正方形ADEF的中心,當點D沿BC邊從點B運動到點C時,點O運動的路徑長為2$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
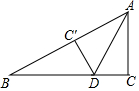 如圖,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,點D是BC邊上一點,連接AD,將△ABC沿AD折疊,點C恰好落在邊AB上的點C′處,則CD的長是$\frac{24}{5}$.
如圖,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,點D是BC邊上一點,連接AD,將△ABC沿AD折疊,點C恰好落在邊AB上的點C′處,則CD的長是$\frac{24}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com