
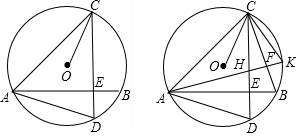
分析 (1)如圖1,作直徑CG,根據(jù)直徑所對(duì)的圓周角是直角,再利用直角三角形兩銳角互余,證明∠ACO=∠BAD;
(2)作輔助線,構(gòu)建等邊三角形,證明△OCK是等邊三角形,所以得∠COK=60°,再根據(jù)同弧所對(duì)的圓心角是圓周角的二倍得∠CAK=30°,證明△AEH∽△AFB,根據(jù)比的值設(shè)EH=2x,BF=$\sqrt{7}$x,由△AFB∽△CFK和30°角的正切,求出CK=$\frac{2\sqrt{21}}{3}$并表示出FH和FK的長(zhǎng),在Rt△AFB中,根據(jù)勾股定理求出x的值,從而得出BF和FC的長(zhǎng),并計(jì)算BC的長(zhǎng)即可.
解答 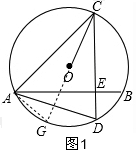 證明:(1)如圖1,作直徑CG,連接AG,
證明:(1)如圖1,作直徑CG,連接AG,
∴∠CAG=90°,
∴∠G+∠ACO=90°,
∵AB⊥CD,
∴∠AED=90°,
∴∠BAD+∠D=90°,
∵∠G=∠D,
∴∠ACO=∠BAD;
(2)如圖2,∵射線CD沿CB翻折交⊙O于K,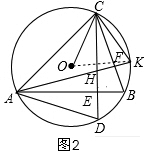
∴∠DCB=∠BCK,
∴$\widehat{BD}=\widehat{BK}$,
∴∠BAD=∠BAK,
∵AB⊥CD,
∴∠BAD+∠D=90°,
∵∠B=∠D,
∴∠B+∠BAK=90°,
∴AK⊥BC,
設(shè)AK交BC于F,連接OK,
∴∠HFC=∠KFC=90°,
∵CF=CF,
∴△HCF≌△KCF,
∴CH=CK,
∵CH=OC,
∴CK=OC=OK,
∴△OCK是等邊三角形,
∴∠COK=60°,
∴∠CAK=30°,
∵∠AEH=∠AFB=90°,∠BAK=∠BAK,
∴△AEH∽△AFB,
∴$\frac{AH}{AB}=\frac{EH}{BF}$=$\frac{4}{2\sqrt{7}}$=$\frac{2}{\sqrt{7}}$,
設(shè)EH=2x,BF=$\sqrt{7}$x,
∵∠BAF=∠BCK,∠AFB=∠CFK,
∴△AFB∽△CFK,
∴$\frac{CF}{AF}=\frac{CK}{AB}$,
∴tan∠CAK=tan30°=$\frac{CF}{AF}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{CK}{AB}=\frac{\sqrt{3}}{3}$,
∴$\frac{CK}{2\sqrt{7}}=\frac{\sqrt{3}}{3}$,
∴CK=$\frac{2\sqrt{21}}{3}$,
sin∠BAK=sin∠BCK=$\frac{EH}{AH}=\frac{FK}{CK}$,
∴$\frac{2x}{4}=\frac{FK}{\frac{2\sqrt{21}}{3}}$,
∴FK=$\frac{\sqrt{21}}{3}$x,
∴FH=FK=$\frac{\sqrt{21}}{3}$x,
在Rt△AFB中,AB2=AF2+BF2,
∴$(2\sqrt{7})^{2}=(4+\frac{\sqrt{21}}{3}x)^{2}+(\sqrt{7}x)^{2}$,
解得:x1=$\frac{2\sqrt{21}}{7}$,x2=-$\frac{3\sqrt{21}}{7}$(舍),
∴BF=$\sqrt{7}$x=$\sqrt{7}×\frac{2\sqrt{21}}{7}$=2$\sqrt{3}$,
FK=$\frac{\sqrt{21}}{3}$x=$\frac{\sqrt{21}}{3}$×$\frac{2\sqrt{21}}{7}$=2,
∴FC=$\sqrt{(\frac{2\sqrt{21}}{3})^{2}-{2}^{2}}$=$\frac{4\sqrt{3}}{3}$,
∴BC=BF+FC=2$\sqrt{3}$+$\frac{4\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$.
答:線段CB的長(zhǎng)為$\frac{10\sqrt{3}}{3}$.
點(diǎn)評(píng) 此題考查了圓周角定理,勾股定理,全等三角形和相似三角形的判定與性質(zhì),以及折疊的性質(zhì),熟練掌握性質(zhì)及定理是解本題的關(guān)鍵,尤其是第二問比較復(fù)雜,同角的三角函數(shù)與三角形相似相結(jié)合,通過(guò)設(shè)未知數(shù),找等量關(guān)系列方程解出未知數(shù)的值,才使問題得以解決.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
| 汽車行駛時(shí)間t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 已知點(diǎn)P在線段AB上,點(diǎn)O在線段AB延長(zhǎng)線上,以點(diǎn)O為圓心,OP為半徑作圓,點(diǎn)C是圓O上的一點(diǎn).
已知點(diǎn)P在線段AB上,點(diǎn)O在線段AB延長(zhǎng)線上,以點(diǎn)O為圓心,OP為半徑作圓,點(diǎn)C是圓O上的一點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
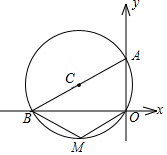 如圖,⊙C過(guò)原點(diǎn),且與兩坐標(biāo)軸分別交于點(diǎn)A,點(diǎn)B,點(diǎn)A的坐標(biāo)為(0,3),M是第三象限內(nèi)弧上一點(diǎn),∠BMO=120°,求⊙C的半徑長(zhǎng).
如圖,⊙C過(guò)原點(diǎn),且與兩坐標(biāo)軸分別交于點(diǎn)A,點(diǎn)B,點(diǎn)A的坐標(biāo)為(0,3),M是第三象限內(nèi)弧上一點(diǎn),∠BMO=120°,求⊙C的半徑長(zhǎng).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
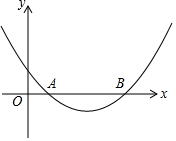 如圖,拋物線y=ax2+bx+1過(guò)A(1,0)、B,(5,0)兩點(diǎn).
如圖,拋物線y=ax2+bx+1過(guò)A(1,0)、B,(5,0)兩點(diǎn).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com