
分析 先根據分式的混合運算順序和法則化簡原式,再將特殊銳角三角函數值代入求得x的值,代入求值即可得.
解答 解:原式=$\frac{(x+2)(x-2)}{x(x+2)^{2}}$÷$\frac{x-2}{x}$
=$\frac{x-2}{x(x+2)}$•$\frac{x}{x-2}$
=$\frac{1}{x+2}$,
當x=2(sin60°-tan45°)=2($\frac{\sqrt{3}}{2}$-1)=$\sqrt{3}$-2時,
原式=$\frac{1}{\sqrt{3}-2+2}$=$\frac{\sqrt{3}}{3}$.
點評 本題主要考查分式的化簡求值和特殊銳角的三角函數值,熟練掌握分式的混合運算順序和法則是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
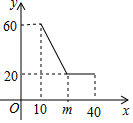 經市場調查,某公司生產的大白公仔的每天的銷售量y(件)與銷售價格x(元/件)之間的函數關系如圖所示.
經市場調查,某公司生產的大白公仔的每天的銷售量y(件)與銷售價格x(元/件)之間的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
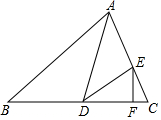 如圖,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E為AC邊上一點,連接DE,∠EAD=∠EDA,EF⊥BC于點F.求∠FED的度數.
如圖,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E為AC邊上一點,連接DE,∠EAD=∠EDA,EF⊥BC于點F.求∠FED的度數.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
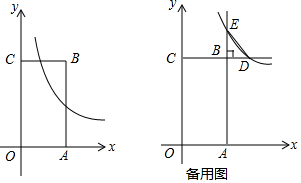
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
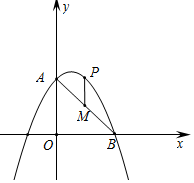
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 尺規作圖并說明作圖依據
尺規作圖并說明作圖依據查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com