
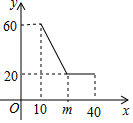
 經市場調查,某公司生產的大白公仔的每天的銷售量y(件)與銷售價格x(元/件)之間的函數關系如圖所示.
經市場調查,某公司生產的大白公仔的每天的銷售量y(件)與銷售價格x(元/件)之間的函數關系如圖所示.分析 (1)利用待定系數法即可解決問題.
(2)列出不等式即可解決問題.
解答 解:(1)設10≤x≤m時,y=kx+b,
由題意$\left\{\begin{array}{l}{mk+b=20}\\{10k+b=60}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{40}{10-m}}\\{b=\frac{200-60m}{10-m}}\end{array}\right.$,
所以當10≤x≤m時,y=$\frac{40}{10-m}$x+$\frac{200-60m}{10-m}$;
當m<x≤40時,y=20;
(2)當m=30時,y=-2x+80,
-2x+80≥24,
∴x≤28,
∴銷售價格的取值范圍為10≤x≤28.
點評 本題考查一次函數的應用、二元一次方程組、不等式等知識,解題的關鍵是熟練掌握待定系數法確定函數解析式,學會用轉化的思想思考問題,所以中考常考題型.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
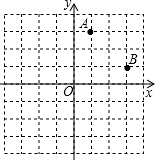 如圖,在平面直角坐標系中,O為原點,每個小方格的邊長為1個單位長度.在第一象限內有橫、縱坐標均為整數的A、B兩點.連接AB,并將線段AB繞點O按順時針旋轉90°到點A1、B1.
如圖,在平面直角坐標系中,O為原點,每個小方格的邊長為1個單位長度.在第一象限內有橫、縱坐標均為整數的A、B兩點.連接AB,并將線段AB繞點O按順時針旋轉90°到點A1、B1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com