
分析 將函數整理成關于x的一元二次方程,然后利用根的判別式列出不等式求解即可.
解答 解:∵y=$\frac{3{x}^{2}+x+2}{{x}^{2}+2x+1}$,
∴y(x2+2x+1)=3x2+x+2,
整理得,(y-3)x2+(2y-1)x+(y-2)=0,
∵關于x的一元二次方程有解,
∴△=b2-4ac=(2y-1)2-4(y-3)(y-2)≥0,
整理得,16y-24≥0,
解得y≤$\frac{3}{2}$,
所以,函數的最小值為$\frac{3}{2}$.
點評 本題考查了二次函數的最值,題目難度較大,將函數整理成關于x的一元二次方程并考慮利用根的判別式求解是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
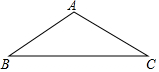 如圖,某廠房人字架屋頂的上弦AB=AC=10米,∠β=α,則該屋頂的跨度BC為( )
如圖,某廠房人字架屋頂的上弦AB=AC=10米,∠β=α,則該屋頂的跨度BC為( )| A. | 10sinα米 | B. | 10cosα米 | C. | 20sinα米 | D. | 20cosα米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 類別/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均數 |
| 甲 | 3 | 4 | 4 | 3 | 4 | 5 | 5 | |
| 乙 | 4 | 3 | 3 | 4 | 3 | 5 | 6 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
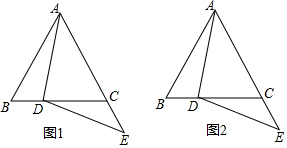 在等邊△ABC中,點D在BC邊上,點E在AC的延長線上,DE=DA(如圖1)
在等邊△ABC中,點D在BC邊上,點E在AC的延長線上,DE=DA(如圖1)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com