
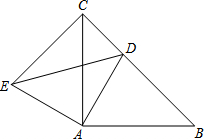
 已知:如圖,等腰△ABC,AB=AC,點D為△ABC的BC邊上一點,連接AD,將線段AD旋轉至AE,使得∠DAE=∠BAC,連接CE.
已知:如圖,等腰△ABC,AB=AC,點D為△ABC的BC邊上一點,連接AD,將線段AD旋轉至AE,使得∠DAE=∠BAC,連接CE.分析 (1)求出∠CAE=∠BAD,AE=AD,根據SAS推出全等即可;
(2)根據全等求出BD,求出BC,根據勾股定理求出AC即可.
解答 (1)證明:根據旋轉得出AE=AD,
∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠CAE=∠BAD,
在△ACE和△ABD中
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠DAB}\\{AE=AD}\end{array}\right.$
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,EC=3,
∴BD=EC=3,
∵CD=1,
∴BC=3+1=4,
∵∠CAB=90°,AC=AB,
∴2AC2=BC2=42=16,
∴AC=2$\sqrt{2}$.
點評 本題考查了勾股定理,全等三角形的性質和判定的應用,能求出△ACE≌△ABD是解此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在一次戶外研學活動中,老師帶領學生去測一條東西流向的河流的寬度(把河兩岸看做平行線,河寬即兩岸之間的垂線段的長度).某同學在河南岸A處觀測到河對岸水邊有一棵樹P,測得P在A北偏東60°方向上,沿河岸向東前行20米到達B處,測得P在B北偏東45°方向上.求河寬(結果保留一位小數.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如圖,在一次戶外研學活動中,老師帶領學生去測一條東西流向的河流的寬度(把河兩岸看做平行線,河寬即兩岸之間的垂線段的長度).某同學在河南岸A處觀測到河對岸水邊有一棵樹P,測得P在A北偏東60°方向上,沿河岸向東前行20米到達B處,測得P在B北偏東45°方向上.求河寬(結果保留一位小數.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 30s | B. | 40s | C. | 50s | D. | 60s |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
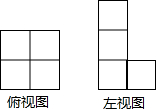 如圖是由一些完全相同的小正方體搭成的幾何體的俯視圖和左視圖,則組成這個幾何體的小正方體的個數是( )
如圖是由一些完全相同的小正方體搭成的幾何體的俯視圖和左視圖,則組成這個幾何體的小正方體的個數是( )| A. | 5或6或7 | B. | 6或7 | C. | 7或8 | D. | 6或7或8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com