
分析 (1)令y=0,使得二次函數變為一元二次方程,然后求出方程中△的值,即可證明結論;
(2)令y=0,使得二次函數變為一元二次方程,然后對方程分解因式,又因此二次函數的圖象與x軸兩個交點的橫坐標都是整數,從而可以求得符合要求的正整數m的值.
解答 解:(1)證明:∵二次函數y=mx2-(m+2)x+2(m≠0),
∴當y=0時,0=mx2-(m+2)x+2(m≠0),
△=[-(m+2)]2-4×m×2=m2+4m+4-8m=m2-4m+4=(m-2)2≥0
∴0=mx2-(m+2)x+2(m≠0)有兩個實數根,
即二次函數y=mx2-(m+2)x+2(m≠0)的圖象與x軸總有交點;
(2)∵二次函數y=mx2-(m+2)x+2(m≠0),
∴當y=0時,0=mx2-(m+2)x+2=(mx-2)(x-1),
∴${x}_{1}=\frac{2}{m},{x}_{2}=1$,
又∵此二次函數的圖象與x軸兩個交點的橫坐標都是整數,
∴正整數m的值是:1或2,
即正整數m的值是1或2.
點評 本題考查拋物線與x軸的交點,解題的關鍵是建立二次函數與一元二次方程之間的關系,然后找出所求問題需要的條件.


科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
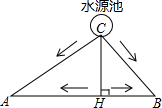 如圖所示,A、B兩塊試驗田相距200米,C為水源地,AC=160m,BC=120m,為了方便灌溉,現有兩種方案修筑水渠.
如圖所示,A、B兩塊試驗田相距200米,C為水源地,AC=160m,BC=120m,為了方便灌溉,現有兩種方案修筑水渠.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com