一次函數y=kx+b的圖象如圖，kx+b=0的解為x=2；不等式kx+b＜0的解集為x＞2． 分析 利用函數圖象，找出函數值為0時的自變量的值即可得到kx+b=0的解；寫出函數圖象在x軸下方所對應的自變量的范圍即得到不等式kx+b＜0的解集．
解答 解：根據函數圖象，當x=2時，y=0，即kx+b=0；
當x＞2時，y＜0，即kx+b＜0，
所以kx+b=0的解為x=2；不等式kx+b＜0的解集為x＞2．
故答案為x=2，x＞2．
點評 本題考查了一次函數與一元一次不等式：一次函數與一元一次不等式的關系從函數的角度看，就是尋求使一次函數y=kx+b的值大于（或小于）0的自變量x的取值范圍；從函數圖象的角度看，就是確定直線y=kx+b在x軸上（或下）方部分所有的點的橫坐標所構成的集合．
一課一練課時達標系列答案科目：初中數學 來源： 題型：選擇題
| A． | a=5，b=6 | B． | a=1，b=-6 | C． | a=-1，b=-6 | D． | a=5，b=-6 |
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
”表示數據輸入、輸出框；用“
”表示數據處理和運算框；用“
”表示數據判斷框（根據條件決定執行兩條路徑中的某一條）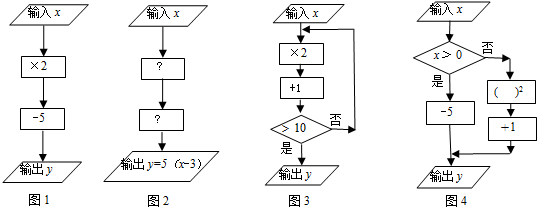
”內，應填-3；第二個運算框“
”內，應填×5；查看答案和解析>>
科目：初中數學 來源： 題型：解答題
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
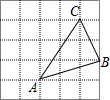如圖，每個小方格都是邊長為1個單位的小正方形，A，B，C三點都是格點（每個小方格的頂點叫格點）．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
如圖是由5個大小相同的小正方體擺成的立體圖形，則從正面看得到的平面圖形是（ ）
