
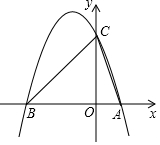
 如圖,在平面直角坐標系中,y=ax2+bx+c(a<0)與x軸交于點A(x1,0),B(x2,0)兩點(x2<0<x1),與y軸正半軸交于點C.已知OA:OB=1:3,OB=OC,△ABC的面積S△ABC=6.
如圖,在平面直角坐標系中,y=ax2+bx+c(a<0)與x軸交于點A(x1,0),B(x2,0)兩點(x2<0<x1),與y軸正半軸交于點C.已知OA:OB=1:3,OB=OC,△ABC的面積S△ABC=6.分析 (1)設OA=x,則OB=OC=3x,依據三角形的面積公式可求得x=1,則A(1,0),B(-3,0),C(0,3),設拋物線的解析式為y=a(x+3)(x-1),將C(0,3)代入求得a的值即可;
(2)當點E在x軸的上方時.設E(x,-x2-2x+3)依據拋物線的對稱性可求得F(-2-x,-x2-2x+3),然后用含x的式子可表示出EH和EF的長,然后依據EF=EH列方程求解即可;當點E在x軸的下方時,EH=|-x2-2x+3|=x2+2x-3.然后由EH=EF列方程求解即可;
(3)當點M在BC的下方時.過點M作直線MD∥BC,交y軸與D,過點D作DE⊥BC,垂足為E.先證明△DCE為等腰直角三角形,然后求得DC的長,從而得到點D的坐標,故此可得到MD的解析式,然后求得直線MD與拋物線的交點坐標即可;當點M在BC的上方時,同理可知CD=4,然后求得直線MD與拋物線的交點坐標即可.
解答 解:(1)設OA=x,則OB=OC=3x.
∵S△ABC=6,
∴$\frac{1}{2}$AB•OC=6,即$\frac{1}{2}$×4x×3x=6,解得x=1.
∴A(1,0),B(-3,0),C(0,3).
設拋物線的解析式為y=a(x+3)(x-1),將C(0,3),代入得:-3a=3,解得a=-1.
∴拋物線的解析式為y=-x2-2x+3.
(2)如圖1所示:當點E在x軸的上方時.
設E(x,-x2-2x+3).
∵拋物線的對稱軸x=-$\frac{b}{2a}$=-1,E(x,-x2-2x+3),
∴F(-2-x,-x2-2x+3).
∴EF=-2-2x.
∵四邊形EFGH為正方形,
∴EH=EF,即-x2-2x+3=-2-2x,解得:x1=-$\sqrt{5}$,x2=$\sqrt{5}$(舍去).
當點E在x軸的下方時,EH=|-x2-2x+3|=x2+2x-3.
由EH=EF得:x2+2x-3=-2-2x,解得:x=-2-$\sqrt{5}$或x=-2+$\sqrt{5}$(舍去).
當x=-$\sqrt{5}$時,EF=-2-2×(-$\sqrt{5}$)=2$\sqrt{5}$-2.
當x=-2-$\sqrt{5}$時,EF=-2-2×(-2-$\sqrt{5}$)=2$\sqrt{5}$+2.
∴正方形的邊長為2$\sqrt{5}$-2或2$\sqrt{5}$+2.
(3)如圖2所示:當點M在BC的下方時,過點M作直線MD∥BC,交y軸與D,過點D作DE⊥BC,垂足為E.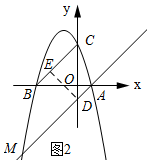
由平移的性質可知BC∥MD.
∵OC=OB,∠BOC=90°,
∴∠BCO=45°.
又∵∠DEC=90°,
∴CD=$\sqrt{2}$DE=$\sqrt{2}$×2$\sqrt{2}$=4.
∴D(0,-1).
∴直線DM的解析式為y=x-1.
將y=x-1與y=-x2-2x+3聯立,解得:x=1或x=-4,
∴點M的坐標為(-4,-5)或(1,0).
當點M在BC的上方時,同理可知CD=4,
∴點D的坐標為(0,7),
∴直線MD的解析式為y=x+7.
將y=x+7與y=-x2-2x+3聯立,方程組無解.
綜上所述點M的坐標為(-4,-5)或(1,0).
點評 本題主要考查的是二次函數的綜合應用,解答本題主要應用了待定系數法求二次函數的解析式,三角形的面積公式,正方形的性質等知識,用含x的式子表示出EF和EH的長度是解答問題(2)的關鍵;求得點D的坐標是解答問題(3)的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 36.2×103m | B. | 3.62×103m | C. | 0.362×104m | D. | 3.62×104m |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com