
 如圖所示,數軸上依次有三點A,O,B,點A位于原點O的左側且相距40個單位長度,BO=30個單位長度,點P從A點出發以3個單位長度/秒的速度勻速向B點運動,點Q從B點出發,以a 個單位長度/秒的速度勻速向A點運動,兩點同時出發(P、Q只在線段AB上運動).若BO表示點O與點B之間的距離,PO表示點P與點O之間的距離,QO表示點Q與點O之間的距離.
如圖所示,數軸上依次有三點A,O,B,點A位于原點O的左側且相距40個單位長度,BO=30個單位長度,點P從A點出發以3個單位長度/秒的速度勻速向B點運動,點Q從B點出發,以a 個單位長度/秒的速度勻速向A點運動,兩點同時出發(P、Q只在線段AB上運動).若BO表示點O與點B之間的距離,PO表示點P與點O之間的距離,QO表示點Q與點O之間的距離.分析 (1)先表示出2秒后P、Q兩點所表示的數,再根據兩點間的距離公式可得;
(2)設t秒后,PO=QO,表示出a=2時,P、Q兩點所表示的數,繼而由PO=QO列出關于t的方程,解之可得;
(3)表示出a=$\frac{9}{4}$且t≠$\frac{40}{3}$時PO、QO的長,由$\frac{PO}{QO}=\frac{|-40+3t|}{|30-\frac{9}{4}t|}$=$\frac{|3t-40|}{|-\frac{3}{4}|•|3t-40|}$=$\frac{4}{3}$可得答案.
解答 解:(1)2秒后點P表示數-40+2×3=-34,點Q表示數30-2a,
則PQ=|30-2a-(-34)|=|64-2a|,
故答案為:|64-2a|;
(2)設t秒后,PO=QO,
當a=2時,點P表示數-40+3t,點Q表示30-2t,
根據題意知,|-40+3t|=|30-2t|,
解得:t=14或t=10,
答:經過10秒或14秒后PO=QO;
(3)當a=$\frac{9}{4}$時,點P表示數-40+3t,點Q表示數30-$\frac{9}{4}$t,
則PO=|-40+3t|、QO=|30-$\frac{9}{4}$t|,
∵t≠$\frac{40}{3}$,
∴$\frac{PO}{QO}=\frac{|-40+3t|}{|30-\frac{9}{4}t|}$=$\frac{|3t-40|}{|-\frac{3}{4}|•|3t-40|}$=$\frac{4}{3}$,
故當a=$\frac{9}{4}$且t≠$\frac{40}{3}$時,$\frac{PO}{QO}$的值不隨時間t的變化而改變.
點評 本題主要考查數軸、兩點間的距離公式及一元一次方程的應用,根據兩點間的距離公式表示出所需線段的長度是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
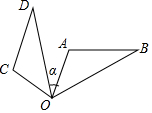 如圖,△OAB繞點O逆時針旋轉70°得到△OCD,若∠A=110°,∠D=30°,則∠α的度數是( )
如圖,△OAB繞點O逆時針旋轉70°得到△OCD,若∠A=110°,∠D=30°,則∠α的度數是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
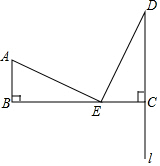 如圖,AB=3,BC=8,AB⊥BC,l⊥BC于點C,點E從B向C運動,過點E作ED⊥AE,交l于D.
如圖,AB=3,BC=8,AB⊥BC,l⊥BC于點C,點E從B向C運動,過點E作ED⊥AE,交l于D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將△ABC繞著點C順時針旋轉50°后得到△DEC.若∠A=40°,∠E=110°,則∠BCD的度數是( )
如圖,將△ABC繞著點C順時針旋轉50°后得到△DEC.若∠A=40°,∠E=110°,則∠BCD的度數是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 最大的負有理數是-1 | |
| B. | 任何有理數的絕對值都是正數 | |
| C. | 0是最小的數 | |
| D. | 如果兩個數互為相反數,那么它們的絕對值相等 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com