
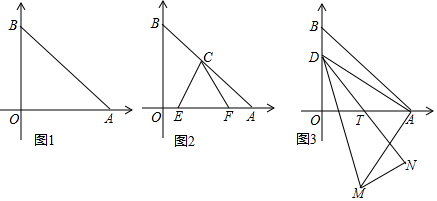
分析 (1)根據(jù)等腰直角三角形的性質(zhì)求出線段OA、OB,可得A、B兩點(diǎn)坐標(biāo),由此即可求出線段AB的中點(diǎn)坐標(biāo).
(2)如圖2中,連接OC,∵BC=AC,∠AOB=90°,∴OC=CA,∠OCB=∠CAF=45°,將△ACF繞點(diǎn)C逆時針旋轉(zhuǎn)90°可得△COM,點(diǎn)M正好在線段OB上.則OM=AF,CM=CF,∠MCO=∠FCA.只要證明△ECM≌△ECF,推出EM=EF,在Rt△MOE中,可得ME2=OM2+OE2,由此即可解決問題.
(3)如圖3中,連接AN.作MG⊥OA于G.設(shè)D(0,a),求出M、N兩點(diǎn)坐標(biāo),利用兩點(diǎn)間的距離公式求出MN,利用二次函數(shù)的性質(zhì)即可解決問題.
解答 解:(1)∵OA=OB,∠AOB=90°,AB=12$\sqrt{2}$,
∴OA=OB=12,
∴A(0,12),B(12,0),
∴線段AB的中點(diǎn)坐標(biāo)為(6,6).
(2)如圖2中,連接OC,
∵BC=AC,∠AOB=90°,
∴OC=CA,∠OCB=∠CAF=45°,
將△ACF繞點(diǎn)C逆時針旋轉(zhuǎn)90°可得△COM,點(diǎn)M正好在線段OB上.
則OM=AF,CM=CF,∠MCO=∠FCA.
∵OC⊥AB,
∴∠OCA=90°,
∵∠ECF=45°,
∴∠ECO+∠FCA=∠ECO+∠MCO=45°,
∴∠MCO=∠ECF,
在△ECM和△ECF中,
$\left\{\begin{array}{l}{EC=EC}\\{∠ECM=∠ECF}\\{CM=CF}\end{array}\right.$,
∴△ECM≌△ECF,
∴EM=EF,
在Rt△MOE中,∵M(jìn)E2=OM2+OE2,
又∵OM=AF,EF=EM,
∴EF2=OE2+AF2.
(3)如圖3中,連接AN.作MG⊥OA于G.設(shè)D(0,a)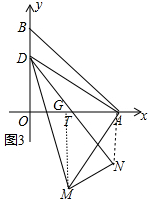
∵∠DAO+∠MAG=90°,∠MAG+∠GMA=90°,
∴∠DAO=∠AMG,
∵AD=AM,∠AOD=∠AGM=90°,
∴△DAO≌△AMG,
∴OD=AG=a,OA=MG=12,
∴M(12-a,-12),
∵OT=TA,DT=TN,∠DTO=∠ATM,
∴△DTO≌△NTA,
∴∠DOT=∠NAT=90°,AN=OD=a,
∴N(12,-a),
∴MN=$\sqrt{{a}^{2}+(12-a)^{2}}$=$\sqrt{2(a-6)^{2}+72}$,
∴a=2時,MN有最小值6$\sqrt{2}$.
點(diǎn)評 本題考查三角形綜合題、全等三角形的判定和性質(zhì)、等腰直角三角形的性質(zhì)、兩點(diǎn)間距離公式、二次函數(shù)的性質(zhì)等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線,構(gòu)造全等三角形解決問題,學(xué)會構(gòu)建二次函數(shù)解決最值問題,屬于中考壓軸題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
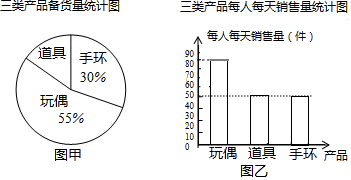
| 產(chǎn)品 | 前三天銷售總量(件) |
| 玩偶 | 720 |
| 道具 | m |
| 手環(huán) | 300 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
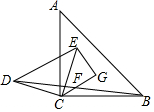 如圖,△ABC和△DEC都是等腰直角三角形,連接BD,F(xiàn)是BD的中點(diǎn),連接CF并延長至G,使FG=CF,連接EC,CE=10,CF=4,EG=6,則S△ABC=2$\sqrt{130}$.
如圖,△ABC和△DEC都是等腰直角三角形,連接BD,F(xiàn)是BD的中點(diǎn),連接CF并延長至G,使FG=CF,連接EC,CE=10,CF=4,EG=6,則S△ABC=2$\sqrt{130}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,拋物線y=-x2+mx+n與x軸分別交于點(diǎn)A(4.0),B(-2.0).與y軸交于點(diǎn)C
如圖,拋物線y=-x2+mx+n與x軸分別交于點(diǎn)A(4.0),B(-2.0).與y軸交于點(diǎn)C查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com