
分析 (1)根據題意可以分求得y甲(元)、y乙(元)與x(筒)之間的函數關系式;
(2)根據(1)中的函數關系式,利用分類討論的數學思想可以解答本題;
(3)根據題意可以分別計算出各種方案的花費情況,即可解答本題.
解答 解:(1)由題意可得,
y甲=50×10+(x-10)×10=10x+400,
y乙=(50×10+10x)×0.9=9x+450,
即y甲=10x+400,y乙=9x+450;
(2)當10x+400<9x+450,
解得,x<50,
當10x+400=9x+450,
解得,x=50,
當10x+400>9x+450,
解得,x>50,
由上可得,當購買不足50筒羽毛球時,甲種優惠辦法更省錢;當購買50筒羽毛球時,兩種優惠辦法一樣;當購買多于50筒羽毛球時,乙種優惠辦法更省錢;
(3)當選擇甲種購買方案時,花費為:10x+400=10×60+400=1000,
當選擇乙種購買方案時,花費為:9x+450=9×60+450=990,
當選擇兩種方案時,花費最低為:10×50+(60-10)×10×0.9=950,
由上可得,同時用兩種優惠辦法購買最省錢.
點評 本題考查一次函數的應用,解答此類問題的關鍵是明確題意,利用分類討論和函數的數學思想解答本題.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
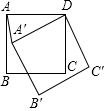 如圖,邊長為4的正方形ABCD繞點D旋轉30°后能與四邊形A′B′C′D重合.
如圖,邊長為4的正方形ABCD繞點D旋轉30°后能與四邊形A′B′C′D重合.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com