
分析 根據分式的混合運算順序和法則依次計算括號內的減法和除法,再解不等式組得出其整數解,選出使分式有意義的x的值代入計算可得.
解答 解:原式=$\frac{x-1}{x+2}$•$\frac{x+2}{(x+1)(x-1)}$=$\frac{1}{x+1}$,
解不等式2x+2>3x,得:x<2,
解不等式$\frac{2x-1}{3}$≥$\frac{1}{2}$x-$\frac{2}{3}$,得:x≥-2,
∴-2≤x<2,
則不等式組的整數解為-2、-1、0、1,
∵x+2≠0且(x+1)(x-1)≠0,
∴x≠±1、-2,
∴x=0時,原式=1.
點評 本題主要考查分式的化簡求值、求一元一次不等式組的整數解,熟練掌握分式的混合運算順序和法則及解不等式組的能力是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
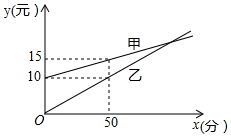 如圖所示,是某電信公司甲、乙兩種業務:每月通話費用y(元)與通話時間x(分)之間的函數關系.某企業的周經理想從兩種業務中選擇一種,如果周經理每個月的通話時間都在100分鐘以上,那么選擇甲種業務合算.
如圖所示,是某電信公司甲、乙兩種業務:每月通話費用y(元)與通話時間x(分)之間的函數關系.某企業的周經理想從兩種業務中選擇一種,如果周經理每個月的通話時間都在100分鐘以上,那么選擇甲種業務合算.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 +(-3xy2)=2x3-5xy2-1+x2
+(-3xy2)=2x3-5xy2-1+x2查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 20° | B. | 20°或30° | C. | 30°或40° | D. | 20°或40° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com