

分析 (1)作AB的中點O,再通過同圓的半徑相等,取OC=AB,則△ABC就是所求作的中線三角形;
(2)如圖2,作輔助線,構建等邊三角形,證明△CDE是等邊三角形,得∠DCE=∠DEC=60°,所以∠ECB=30°設EF=x,分別表示BC=2$\sqrt{3}$x,AC=2DC=2CE=4x,代入求比值即可;
(3)①如圖3,當△APQ為中線三角形,此時PQ=AE,因為點P、Q同時從點A出發,且以相同的速度運動,所以AB+BP=AD+DQ,則BP=DQ,根據等式的性質和正方形的邊長相等得:PC=CQ,再證明△ABP≌△ADQ,得AP=AQ,由等腰三角形三線合一的性質得:AE⊥PQ,∠PAE=∠QAE,并證明AE與AC共線,
設CE=x,表示PQ=AE=2x,根據勾股定理列方程求出x的值,代入面積公式求三角形的面積即可.
②如圖4,當AP=EQ時,作輔助線,設AG=x,則AP=AQ=4x,先表示AP與高QG的長,利用面積公式可計算結果.
解答 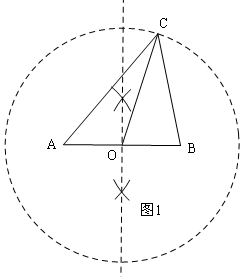 解:(1)作法:①作AB的中垂線,交AB于O,
解:(1)作法:①作AB的中垂線,交AB于O,
②以O為圓心,以AB為半徑畫圓,在圓上任意取一點C,
③連接AC、BC,
則△ABC就是所求作的中線三角形;
(2)如圖2,取BD的中點E,連接CE,過E作EF⊥BC于F,
∵∠C=90°,
∴CE=$\frac{1}{2}$BD=BE,
∵D是AC的中點,E是BD的中點,
∴CD=$\frac{1}{2}$AC,DE=$\frac{1}{2}$BD,
∵AC=BD,
∴CD=DE=CE,
∴△CDE是等邊三角形,
∴∠DCE=∠DEC=60°,
∴∠ECB=90°-60°=30°,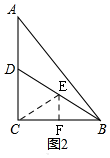
設EF=x,則EC=BE=2x,CF=$\sqrt{3}$x,
同理BF=$\sqrt{3}$x,
∴BC=2$\sqrt{3}$x,AC=2DC=2CE=4x,
∴$\frac{BC}{AC}=\frac{2\sqrt{3}x}{4x}$=$\frac{\sqrt{3}}{2}$;
(3)有兩種情況:
①如圖3,當△APQ為中線三角形,此時PQ=AE,
由題意得:AB+BP=AD+DQ,
∵四邊形ABCD為正方形,
∴AB=AD=BC=CD,
∴BP=DQ,
∴BC-BP=CD-DQ,
∴PC=CQ,
∵∠B=∠D=90°,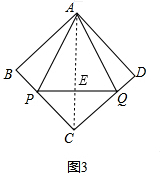
∴△ABP≌△ADQ,
∴AP=AQ,
∵AE為中線,
∴AE⊥PQ,∠PAE=∠QAE,
連接AC,
∵AP=AQ,PC=CQ,
∴AC為PQ的中垂線,
∴AE與AC共線,
∵四邊形ABCD為正方形,
∴∠BCD=90°,
∵E是PQ的中點,
∴CE=$\frac{1}{2}$PQ=PE=EQ,
設CE=x,則PE=EQ=x,PQ=AE=2x,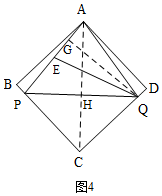
Rt△ABC中,AB=6,
∴62+62=AC2=(AE+CE)2,
72=(2x+x)2,
x=$±2\sqrt{2}$,
∵x>0,
∴PQ=AE=2x=4$\sqrt{2}$,
∴S△APQ=$\frac{1}{2}$PQ•AE=$\frac{1}{2}$×4$\sqrt{2}$×4$\sqrt{2}$=16.
②如圖4,當△APQ為中線三角形,此時AP=EQ,
過E作QG⊥AP于G,
∵AP=AQ=EQ,
∴AG=EG,
∵AE=EP,
設AG=x,則AP=AQ=4x,
∴QG=$\sqrt{A{Q}^{2}-A{G}^{2}}$=$\sqrt{(4x)^{2}-{x}^{2}}$=$\sqrt{15}$x,
連接AC交PQ于H,則AC⊥PQ,
設CH=a,則QH=a,AH=6$\sqrt{2}$-a,
Rt△AHQ中,AQ2=AH2+HQ2,
∴$(4x)^{2}=(6\sqrt{2}-a)^{2}+{a}^{2}$,
16x2=72-12$\sqrt{2}$a+2a2 ①,
S△APQ=$\frac{1}{2}$AP•QG=$\frac{1}{2}$PQ•AH,
4x$•\sqrt{15}$x=2a(6$\sqrt{2}$-a),
$4\sqrt{15}{x}^{2}$=12$\sqrt{2}$a-2a2 ②,
由①和②得:16x2=72-4$\sqrt{15}$x2,
(16+4$\sqrt{15}$)x2=72,
x2=18(4-$\sqrt{15}$),
∴S△APQ=$\frac{1}{2}$AP•QG=$\frac{1}{2}$•4x$•\sqrt{15}$x=2$\sqrt{15}$×18(4-$\sqrt{15}$)=144$\sqrt{15}$-540;
綜上所述,當△APQ是“中線三角形”時,△APQ的面積是16或144$\sqrt{15}$-540.
點評 本題是四邊形的綜合題,考查了正方形的性質、直角三角形斜邊中線的性質,等腰三角形的性質以及三角形全等的性質和判定,又是一道新定義的閱讀理解問題及尺規作圖題,綜合性較強;熟練掌握性質和定理是關鍵,并注意理解和運用已知的“中線長恰好等于這邊的長”這一條件.


科目:初中數學 來源: 題型:解答題
 如圖,拋物線頂點坐標為點C(2,8),交x軸于點A(6,0),交y軸于點B.
如圖,拋物線頂點坐標為點C(2,8),交x軸于點A(6,0),交y軸于點B.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,BD平分∠ABC,BC的中垂線交BC于點E,交BD于點F,連接CF.
如圖,△ABC中,BD平分∠ABC,BC的中垂線交BC于點E,交BD于點F,連接CF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點C在線段AB上,點M、N分別是AC、BC的中點.
如圖,點C在線段AB上,點M、N分別是AC、BC的中點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )
如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-5,0),對稱軸為直線x=-2,給出四個結論:
如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-5,0),對稱軸為直線x=-2,給出四個結論:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
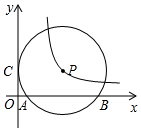 如圖,⊙P與y軸相切于點C(0,3),與x軸相交于點A(1,0),B(9,0).雙曲線y=$\frac{k}{x}$恰好經過圓心P,那么k的值是15.
如圖,⊙P與y軸相切于點C(0,3),與x軸相交于點A(1,0),B(9,0).雙曲線y=$\frac{k}{x}$恰好經過圓心P,那么k的值是15.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,△ABC的三個頂點分別為A(2,3),B(3,1),C(-2,-2).
如圖,在平面直角坐標系中,△ABC的三個頂點分別為A(2,3),B(3,1),C(-2,-2).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com