
 如圖,點C在線段AB上,點M、N分別是AC、BC的中點.
如圖,點C在線段AB上,點M、N分別是AC、BC的中點.分析 (1)由中點的性質得MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,根據MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)可得答案;
(2)與(1)同理;
(3)根據中點的性質得MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,結合圖形依據MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)可得答案.
解答 解:(1)∵M、N分別是AC、BC的中點,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC=9cm,CB=6cm,
∴MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$(9+6)=7.5cm;
(2)∵M、N分別是AC、BC的中點,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC+CB=acm,
∴MN=MC+CN=AC+CB=acm)=$\frac{1}{2}$a(cm);
(3)MN=$\frac{1}{2}$b,
如圖,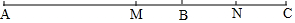
∵M、N分別是AC、BC的中點,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC-BC=b cm,
∴MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$b.
點評 本題主要考查兩點間的距離,掌握線段的中點的性質、線段的和差運算是解題的關鍵.


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點O為平面直角坐標系的原點,點A的坐標為(6,8),點B的坐標為(12,0).
如圖,點O為平面直角坐標系的原點,點A的坐標為(6,8),點B的坐標為(12,0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x≥-2 | B. | x>-2 | C. | x<-2 | D. | x≤-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
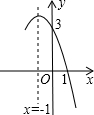 拋物線y=-x2+bx+c的部分圖象如圖所示,對稱軸為x=-1,若y>0,則x的取值范圍是( )
拋物線y=-x2+bx+c的部分圖象如圖所示,對稱軸為x=-1,若y>0,則x的取值范圍是( )| A. | -3<x<1 | B. | x<-3或x>1 | C. | -4<x<l | D. | x<-4或x>1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,正方形ABCD的面積為12,△ABE是等邊三角形,點E在正方形ABCD內,在對角線AC上有一點P,使PD+PE最小,則這個最小值為( )
如圖,正方形ABCD的面積為12,△ABE是等邊三角形,點E在正方形ABCD內,在對角線AC上有一點P,使PD+PE最小,則這個最小值為( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com