
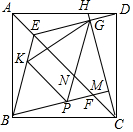
 如圖,四邊形ABCD為正方形,H是AD上任意一點,連接CH,過B作BM⊥CH于M,交AC于F,過D作DE∥BM交AC于E,交CH于G,在線段BF上作PF=DG,連接PG,BE,其中PG交AC于N點,K為BE上一點,連接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值為$\frac{\sqrt{505}}{15}$.
如圖,四邊形ABCD為正方形,H是AD上任意一點,連接CH,過B作BM⊥CH于M,交AC于F,過D作DE∥BM交AC于E,交CH于G,在線段BF上作PF=DG,連接PG,BE,其中PG交AC于N點,K為BE上一點,連接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值為$\frac{\sqrt{505}}{15}$. 分析 連接DF,構建菱形EBFD和平行四邊形GPFD,證明KP∥EF,得△BPK∽△BFE,列比例式為$\frac{PK}{EF}=\frac{BP}{BF}$=$\frac{3}{5}$,設BP=3x,BF=5x,則PF=CM=DG=2x,EG=3x,根據BM=12列方程解出x的值,計算EG的長;
設AC與KG交于點O,過K作KP⊥AC于P,過G作GQ⊥AC于Q,則KP∥GQ,根據同角的三角函數求KP、GQ、OP、OQ的長,證明△KIO∽△GQO,根據相似比為2:3分別求OK、OG的長,并相加即可得KG的長,最后計算比值即可.
解答 解:連接DF,
∵四邊形ABCD為正方形,
∴BC=CD,∠BCD=90°,
∴∠BCM+∠MCD=90°,
∵BM⊥CH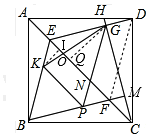
∴∠BMC=90°,
∴∠BCM+∠MBC=90°,
∴∠MCD=∠MBC,
∵DE∥BM,
∴∠DGC=∠BMG=90°,
∴∠DGC=∠BMC=90°,
∴△BMC≌△CGD,
∴BM=CG=12,CM=DG,
∵PF=DG,
∴PF=DG=CM,
在△ABE和△ADE中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAE=45°}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ADE(SAS),
∴BE=ED,∠AEB=∠AED,
∴∠BEF=∠FED,
∵DE∥BM,
∴∠DEF=∠EFB,
∴∠BEF=∠EFB,
∴BE=BF,
∴BE=BF=ED,
∴四邊形EBFD是菱形,
∴∠BFE=∠EFD,
∴GD=PF,GD∥PF,
∴四邊形GPFD是平行四邊形,
∴GP∥DF,
∴∠BPG=∠BFD,
∵∠BPK=∠KPG,
∴2∠BPK=2∠BFE,
∴∠BPK=∠BFE,
∴PK∥EF,
∴△BPK∽△BFE,
∴$\frac{PK}{EF}=\frac{BP}{BF}$=$\frac{3}{5}$,
設BP=3x,BF=5x,則PF=CM=DG=2x,EG=3x,
∵FM∥DE,
∴△CFM∽△CEG,
∴$\frac{FM}{EG}=\frac{CM}{CG}$,
∴$\frac{FM}{3x}=\frac{2x}{12}$,
∴FM=$\frac{{x}^{2}}{2}$,
∵BM=12,
∴BF+FM=12,
5x+$\frac{{x}^{2}}{2}$=12,
解得:x1=2,x2=-12(舍),
∴EG=3x=6;FM=$\frac{{2}^{2}}{2}$=2,CM=2x=4,
∵∠BKP=∠BPK,
∴BK=BP=3x=6,
∵BF=5x=10,
∴EK=10-6=4,
設AC與KG交于點O,過K作KI⊥AC于I,過G作GQ⊥AC于Q,則KI∥GQ,
∵∠BEF=∠DEF,
∴$\frac{EK}{EG}=\frac{OK}{OG}$=$\frac{4}{6}$=$\frac{2}{3}$,
∵∠BEF=∠BFE=∠CFM,
∴tan∠BEF=tan∠CFM=$\frac{CM}{FM}$=$\frac{KI}{EI}$=$\frac{4}{2}$=2,
∵EK=4,
∴KI=$\frac{8\sqrt{5}}{5}$,EI=$\frac{4\sqrt{5}}{5}$,
同理得:GQ=$\frac{12\sqrt{5}}{5}$,EQ=$\frac{6\sqrt{5}}{5}$,
∴IQ=EQ-EI=$\frac{6\sqrt{5}}{5}$-$\frac{4\sqrt{5}}{5}$=$\frac{2\sqrt{5}}{5}$,
∵KI∥GQ,
∴△KIO∽△GQO,
∴$\frac{OI}{OQ}$=$\frac{OK}{OG}$=$\frac{2}{3}$,
∴$\frac{OI}{IQ}$,
∴OI=$\frac{2}{5}$×IQ=$\frac{2}{5}$×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{25}$,
由勾股定理得:OK=$\sqrt{K{P}^{2}+O{P}^{2}}$=$\sqrt{(\frac{8\sqrt{5}}{5})^{2}+(\frac{4\sqrt{5}}{25})^{2}}$=$\frac{4\sqrt{505}}{25}$,
∴OG=$\frac{6\sqrt{505}}{25}$,
∴KG=OK+OG=$\frac{2\sqrt{505}}{5}$,
∴$\frac{KG}{EG}$=$\frac{\frac{2\sqrt{505}}{5}}{6}$=$\frac{\sqrt{505}}{15}$;
故答案為:$\frac{\sqrt{505}}{15}$.
點評 本題考查的是正方形的性質、菱形和平行四邊形的判定和性質、全等三角形的判定和性質以及相似三角形的判定和性質,正確作出輔助性、靈活運用相關的性質定理和判定定理是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 甲型號LED照明燈 | 乙型號LED照明燈 | |
| 進價(元/只) | 20 | 40 |
| 售價(元/只) | 30 | 55 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a(1+9.6%+10%) | B. | a(1+9.6%×10%) | C. | a(1+9.6%)(1+10%) | D. | a(1+9.6%)2(1+10%) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
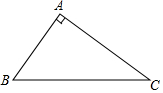 如圖,已知△ABC中,已知△ABC中,∠BAC=90°,∠ABC=54°,AC=10.
如圖,已知△ABC中,已知△ABC中,∠BAC=90°,∠ABC=54°,AC=10.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,以△ABC的AB邊為直徑作⊙O,交BC于點D,過點D作⊙O的切線DE,交AC于點E,且DE⊥AC,連接EO.
如圖,以△ABC的AB邊為直徑作⊙O,交BC于點D,過點D作⊙O的切線DE,交AC于點E,且DE⊥AC,連接EO.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com