
 如圖,以△ABC的AB邊為直徑作⊙O,交BC于點(diǎn)D,過點(diǎn)D作⊙O的切線DE,交AC于點(diǎn)E,且DE⊥AC,連接EO.
如圖,以△ABC的AB邊為直徑作⊙O,交BC于點(diǎn)D,過點(diǎn)D作⊙O的切線DE,交AC于點(diǎn)E,且DE⊥AC,連接EO.分析 (1)連接OD,如圖,根據(jù)切線的性質(zhì)得OD⊥DE,則可判斷OD∥AC,根據(jù)平行線的性質(zhì)得∠C=∠1,加上∠B=∠1,則∠C=∠B,于是可判定AB=AC;
(2)連接AD,如圖2.先利用三角形中位線性質(zhì)得到OD=$\frac{5}{2}$,再證明△CDE∽△DAE,利用相似比求出DE=2,則利用正切定義得到$tan∠2=\frac{DE}{OD}=\frac{4}{5}$,然后利用OD∥AC得到∠AEO=∠2,所以得到$tan∠AEO=\frac{4}{5}$.
解答 (1)證明:連接OD,如圖,
∵OD是⊙O半徑,DE為⊙O的切線,
∴OD⊥DE,
∵DE⊥AC,
∴OD∥AC,
∴∠C=∠1,
∵OD=OB,
∴∠B=∠1,
∴∠C=∠B,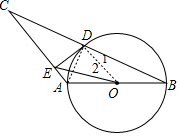
∴AB=AC;
(2)連接AD,如圖.
∵AB=5,AE=1,
∴OD=$\frac{5}{2}$,AC=AB=5,EC=4.
∵AB是⊙O的直徑,
∴∠ADB=90°,
∴∠ADE+∠CDE=90°,
∵∠ADE+∠DAE=90°,
∴∠DAE=∠CDE,
∴△CDE∽△DAE,
∴DE2=CE•AE=4×1=4,
∴DE=2,
在Rt△EDO中,$tan∠2=\frac{DE}{OD}=\frac{4}{5}$,
∵OD∥AC,
∴∠AEO=∠2.
∴$tan∠AEO=\frac{4}{5}$.
點(diǎn)評 本題考查了切線的性質(zhì):圓的切線垂直于經(jīng)過切點(diǎn)的半徑.若出現(xiàn)圓的切線,必連過切點(diǎn)的半徑,構(gòu)造定理圖,得出垂直關(guān)系.簡記作:見切點(diǎn),連半徑,見垂直.也考查了相似三角形的判定與性質(zhì).


 學(xué)練快車道快樂假期寒假作業(yè)系列答案
學(xué)練快車道快樂假期寒假作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
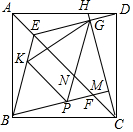 如圖,四邊形ABCD為正方形,H是AD上任意一點(diǎn),連接CH,過B作BM⊥CH于M,交AC于F,過D作DE∥BM交AC于E,交CH于G,在線段BF上作PF=DG,連接PG,BE,其中PG交AC于N點(diǎn),K為BE上一點(diǎn),連接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值為$\frac{\sqrt{505}}{15}$.
如圖,四邊形ABCD為正方形,H是AD上任意一點(diǎn),連接CH,過B作BM⊥CH于M,交AC于F,過D作DE∥BM交AC于E,交CH于G,在線段BF上作PF=DG,連接PG,BE,其中PG交AC于N點(diǎn),K為BE上一點(diǎn),連接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值為$\frac{\sqrt{505}}{15}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
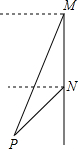 如圖,輪船沿正南方向以30海里/時的速度勻速航行,在M處觀測到燈塔P在西偏南68°方向上,航行2小時后到達(dá)N處,觀測燈塔P在西偏南46°方向上,若該船繼續(xù)向南航行至離燈塔最近位置,則此時輪船離燈塔的距離約為41.682(由科學(xué)計算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)
如圖,輪船沿正南方向以30海里/時的速度勻速航行,在M處觀測到燈塔P在西偏南68°方向上,航行2小時后到達(dá)N處,觀測燈塔P在西偏南46°方向上,若該船繼續(xù)向南航行至離燈塔最近位置,則此時輪船離燈塔的距離約為41.682(由科學(xué)計算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
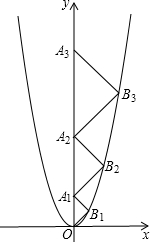 如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)A1,A2,A3,…,An在y軸的正半軸上,點(diǎn)B1,B2,B3,…,Bn在二次函數(shù)y=x2位于第一象限的圖象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,則:
如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)A1,A2,A3,…,An在y軸的正半軸上,點(diǎn)B1,B2,B3,…,Bn在二次函數(shù)y=x2位于第一象限的圖象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,則:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| 柑橘總質(zhì)量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 損壞柑橘質(zhì)量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘損壞的頻率$\frac{m}{n}$ (結(jié)果保留小數(shù)點(diǎn)后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,擬從點(diǎn)A修建一條小徑到邊BC,若要使修建小徑使用的材料最少,則過點(diǎn)A作AD⊥BC于點(diǎn)D,線段AD即為所求小徑的位置,這樣畫的理由是垂線段最短.
如圖,擬從點(diǎn)A修建一條小徑到邊BC,若要使修建小徑使用的材料最少,則過點(diǎn)A作AD⊥BC于點(diǎn)D,線段AD即為所求小徑的位置,這樣畫的理由是垂線段最短.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 無解 | B. | 有一組解 | C. | 有無窮多解 | D. | 不確定 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com