
 如圖,在平面直角坐標系中,點O是坐標原點,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,將△OAB沿直線AB翻折,得到△CAB,點O與點C對應.
如圖,在平面直角坐標系中,點O是坐標原點,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,將△OAB沿直線AB翻折,得到△CAB,點O與點C對應.分析 (1)根據翻轉變換的性質解答;
(2)先根據題意補全圖形,根據直角三角形的性質求出BE;
(3)分B是等腰三角形△BEF的頂角頂點、E為等腰三角形△BEF的頂角頂點兩種情況,根據等腰三角形的性質、翻轉變換的性質計算即可.
解答  解:(1)∵∠OBA=60°,
解:(1)∵∠OBA=60°,
∴∠OAB=30°,
由翻轉變換的性質可知,∠BAC=∠OAB=30°,
故答案為:30;
(2)補全圖形如圖1,
∵BE⊥x軸,
∴∠OBE=90°
∵∠OBA=60°,
∴∠EBA=30°,
∴∠EBA=∠BAC=30°,
∴AE=BE,
∵∠ABC=∠OBA=60°,
∴∠EBC=∠ABC-∠EBA=30°,
又∵∠C=∠FOB=90°,
∴CE=$\frac{1}{2}$BE,
又∵AC=AE+EC=6,
∴AC=BE+$\frac{1}{2}$BE=6,
∴BE=4;
(3)①當B是等腰三角形△BEF的頂角頂點時,如圖2,
當BF=BE時,OF=CE=2,
∴t=2÷2=1,
當BF=BE=4時,如圖3,
∵AF=AB-BF=4$\sqrt{3}$-4,
∴t=$\frac{OA+OF}{2}$=$\frac{6+4\sqrt{3}-4}{2}$=1+2$\sqrt{3}$,
②當E為等腰三角形△BEF的頂角頂點時,如圖4,
∵∠ABE=30°,∠BAC=30°,
則當F運動到A點時,即AE=BE,
∴△BEF為等腰三角形,即t=6÷2=3,
當EF=BE時,由(2)得:AE=BE,
∴EF=AE=4,又∵∠OAE=60°,
∴△AEF為等邊三角形,
∴A F=AE=4
∴O F=AO-AF=2,
∴F與圖2中F重合,此時 t=1,
所以在點F的運動過程中,當t=1(秒)或t=3(秒)或t=(1+2$\sqrt{3}$)(秒)時,△BEF是以BE為腰的等腰三角形.
點評 本題考查的是等腰三角形的判定和性質、直角三角形的性質、翻轉變換的性質,掌握翻轉變換的性質、靈活運用分情況討論思想是解題的關鍵.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ABC,∠ACB的平分線交于點O,D是∠ACB外角與內角∠ABC平分線交點,E是∠ABC,∠ACB外角平分線交點,若∠BOC=120°,則∠D=( )度.
如圖,在△ABC中,∠ABC,∠ACB的平分線交于點O,D是∠ACB外角與內角∠ABC平分線交點,E是∠ABC,∠ACB外角平分線交點,若∠BOC=120°,則∠D=( )度.| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
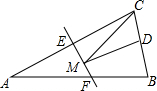 如圖,等腰三角形ABC的底邊BC長為4,面積是16,腰AC的垂直平分線EF分別交AC,AB邊于E,F點,若點D為BC邊的中點,點M為線段EF上一動點,則△CDM周長的最小值為10.
如圖,等腰三角形ABC的底邊BC長為4,面積是16,腰AC的垂直平分線EF分別交AC,AB邊于E,F點,若點D為BC邊的中點,點M為線段EF上一動點,則△CDM周長的最小值為10.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 會員年卡類型 | 辦卡費用(元) | 每次游泳收費(元) |
| A類 | 100 | 30 |
| B類 | 200 | 25 |
| C類 | 500 | 15 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知⊙O是銳角△ABC的外接圓,BE,CF分別是AC,AB邊上的高,自垂足E,F分別作AB,AC的垂線,垂足為G,H,設EG與FH相交于K.
如圖,已知⊙O是銳角△ABC的外接圓,BE,CF分別是AC,AB邊上的高,自垂足E,F分別作AB,AC的垂線,垂足為G,H,設EG與FH相交于K.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com