

分析 (1)①過(guò)點(diǎn)C作CE⊥CB,與直線MN于點(diǎn)E,據(jù)此作圖即可;
②先根據(jù)ASA判定△CAE≌△CDB,得出AE=DB,CE=CB,進(jìn)而得到△ECB為等腰直角三角形,得出BE=$\sqrt{2}$CB,再根據(jù)BE=AE+AB,得到BE=BD+AB,即可得出BD+AB=$\sqrt{2}$CB;
(2)①過(guò)點(diǎn)C作CE⊥CB,與直線MN于點(diǎn)E,根據(jù)∠ACE=∠DCB,∠D=∠CAE,即可判定△ACE∽△DCB,進(jìn)而得出$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,從而得到$\sqrt{3}$BE=2CB,$\sqrt{3}$AE=BD,最后根據(jù)AB=AE+BE,得出$\sqrt{3}$AB=$\sqrt{3}$AE+$\sqrt{3}$BE,即$\sqrt{3}$AB=BD+2CB;
②過(guò)點(diǎn)C作CE⊥CB,與直線MN于點(diǎn)E,根據(jù)∠ACE=∠DCB,∠D=∠CAE,判定△ACE∽△DCB,進(jìn)而得出$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,即可得到$\sqrt{3}$BE=2CB,$\sqrt{3}$AE=BD,最后根據(jù)AB=AE-BE,得出$\sqrt{3}$AB=$\sqrt{3}$AE-$\sqrt{3}$BE,即$\sqrt{3}$AB=BD-2CB.
解答  解:(1)①補(bǔ)全圖形如圖1所示;
解:(1)①補(bǔ)全圖形如圖1所示;
②∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN于點(diǎn)B,
∴∠ABD=90°,
∴∠BAC+∠D=180°.
又∵∠BAC+∠EAC=180°,
∴∠D=∠EAC.
在△CAE和△CDB中,
$\left\{\begin{array}{l}{∠ACE=∠DCB}\\{CA=CD}\\{∠EAC=∠D}\end{array}\right.$
∴△CAE≌△CDB,
∴AE=DB,CE=CB,
∴△ECB為等腰直角三角形,
∴BE=$\sqrt{2}$CB.
又∵BE=AE+AB,
∴BE=BD+AB,
即BD+AB=$\sqrt{2}$CB,
故答案為:BD+AB=$\sqrt{2}$CB;
(2)①證明:如圖2,過(guò)點(diǎn)C作CE⊥CB,與直線MN于點(diǎn)E,
∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN,
∴∠DBF=90°=∠ACF,
又∵∠DFB=∠AFC,
∴∠D=∠CAE,
∴△ACE∽△DCB,
又∵CD=$\sqrt{3}$AC,
∴$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,
∴Rt△BCE中,$\frac{CB}{BE}$=$\frac{\sqrt{3}}{2}$,即$\sqrt{3}$BE=2CB,
∵$\frac{BD}{EA}$=$\sqrt{3}$,
∴$\sqrt{3}$AE=BD,
∵AB=AE+BE,
∴$\sqrt{3}$AB=$\sqrt{3}$AE+$\sqrt{3}$BE,
即$\sqrt{3}$AB=BD+2CB;
②線段BD、AB、CB滿(mǎn)足的數(shù)量關(guān)系是:BD-2CB=$\sqrt{3}$AB.
理由:如圖3,過(guò)點(diǎn)C作CE⊥CB,與直線MN于點(diǎn)E,
∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN,
∴∠DBA=90°=∠ACD,
又∵∠AFB=∠DFC,
∴∠D=∠CAE,
∴△ACE∽△DCB,
又∵CD=$\sqrt{3}$AC,
∴$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,
∴Rt△BCE中,$\frac{CB}{BE}$=$\frac{\sqrt{3}}{2}$,即$\sqrt{3}$BE=2CB,
∵$\frac{BD}{EA}$=$\sqrt{3}$,
∴$\sqrt{3}$AE=BD,
∵AB=AE-BE,
∴$\sqrt{3}$AB=$\sqrt{3}$AE-$\sqrt{3}$BE,
即$\sqrt{3}$AB=BD-2CB.
故答案為:$\sqrt{3}$AB=BD-2CB.
點(diǎn)評(píng) 本題屬于三角形作圖,主要考查了全等三角形的判定與性質(zhì),相似三角形的判定與性質(zhì)以及等腰直角三角形的性質(zhì)的綜合應(yīng)用,解決問(wèn)題的關(guān)鍵是作輔助線構(gòu)造全等三角形和相似三角形,運(yùn)用全等三角形的對(duì)應(yīng)邊相等以及相似三角形的對(duì)應(yīng)邊成比例進(jìn)行推導(dǎo)計(jì)算.


 能力評(píng)價(jià)系列答案
能力評(píng)價(jià)系列答案 唐印文化課時(shí)測(cè)評(píng)系列答案
唐印文化課時(shí)測(cè)評(píng)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
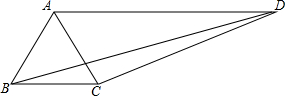 在四邊形ABCD中,連接對(duì)角線AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,則BD=3$\sqrt{13}$.
在四邊形ABCD中,連接對(duì)角線AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,則BD=3$\sqrt{13}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
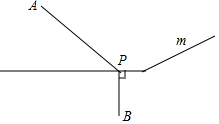 如圖所示,在兩個(gè)村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現(xiàn)要在河邊修一個(gè)水泵站,同時(shí)向A,B兩村供水,為了節(jié)約建設(shè)的費(fèi)用,就要使所鋪設(shè)的管道最短,某人甲提出了這樣的建議:從點(diǎn)B向河道作垂線交m于點(diǎn)P,則點(diǎn)P為水泵站的位置.
如圖所示,在兩個(gè)村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現(xiàn)要在河邊修一個(gè)水泵站,同時(shí)向A,B兩村供水,為了節(jié)約建設(shè)的費(fèi)用,就要使所鋪設(shè)的管道最短,某人甲提出了這樣的建議:從點(diǎn)B向河道作垂線交m于點(diǎn)P,則點(diǎn)P為水泵站的位置.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
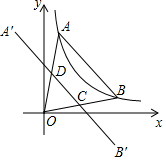 如圖,點(diǎn)A、B在函數(shù)y=$\frac{1}{x}$(x>0)的圖象上,點(diǎn)A在點(diǎn)B的左側(cè),且OA=OB,點(diǎn)A關(guān)于y軸的對(duì)稱(chēng)點(diǎn)為A′,點(diǎn)B關(guān)于x軸的對(duì)稱(chēng)點(diǎn)為B′,連接A′B′分別交OA、OB于點(diǎn)D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點(diǎn)A的坐標(biāo)為($\frac{1}{2}$,2),點(diǎn)C的坐標(biāo)為($\frac{6}{5}$,$\frac{3}{10}$).
如圖,點(diǎn)A、B在函數(shù)y=$\frac{1}{x}$(x>0)的圖象上,點(diǎn)A在點(diǎn)B的左側(cè),且OA=OB,點(diǎn)A關(guān)于y軸的對(duì)稱(chēng)點(diǎn)為A′,點(diǎn)B關(guān)于x軸的對(duì)稱(chēng)點(diǎn)為B′,連接A′B′分別交OA、OB于點(diǎn)D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點(diǎn)A的坐標(biāo)為($\frac{1}{2}$,2),點(diǎn)C的坐標(biāo)為($\frac{6}{5}$,$\frac{3}{10}$).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com