
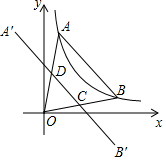
 如圖,點A、B在函數y=$\frac{1}{x}$(x>0)的圖象上,點A在點B的左側,且OA=OB,點A關于y軸的對稱點為A′,點B關于x軸的對稱點為B′,連接A′B′分別交OA、OB于點D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點A的坐標為($\frac{1}{2}$,2),點C的坐標為($\frac{6}{5}$,$\frac{3}{10}$).
如圖,點A、B在函數y=$\frac{1}{x}$(x>0)的圖象上,點A在點B的左側,且OA=OB,點A關于y軸的對稱點為A′,點B關于x軸的對稱點為B′,連接A′B′分別交OA、OB于點D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點A的坐標為($\frac{1}{2}$,2),點C的坐標為($\frac{6}{5}$,$\frac{3}{10}$). 分析 因為反比例函數y=$\frac{1}{x}$,關于直線y=x對稱,因為OA=OB,所以A、B關于直線y=x對稱,可以設點A的坐標為(m,$\frac{1}{m}$),則點B的坐標為($\frac{1}{m}$,m),則點A′的坐標為(-m,$\frac{1}{m}$),點B′的坐標為($\frac{1}{m}$,-m),求出直線OB、A′B′的解析式,解方程組求出點C的坐標,求出線段CD、AB,列出方程求出m即可解決問題.
解答 解:∵反比例函數y=$\frac{1}{x}$,關于直線y=x對稱,
∵OA=OB,
∴A、B關于直線y=x對稱,
設點A的坐標為(m,$\frac{1}{m}$),則點B的坐標為($\frac{1}{m}$,m),則點A′的坐標為(-m,$\frac{1}{m}$),點B′的坐標為($\frac{1}{m}$,-m),
∴直線OB的解析式為y=m2x,
直線A′B′的解析式為y=-x+$\frac{1}{m}$-m,
由$\left\{\begin{array}{l}{y={m}^{2}x}\\{y=-x+\frac{1}{m}-m}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1-{m}^{2}}{m({m}^{2}+1)}}\\{y=\frac{m(1-{m}^{2})}{{m}^{2}+1}}\end{array}\right.$,
∴C[$\frac{1-{m}^{2}}{m({m}^{2}+1)}$,$\frac{m(1-{m}^{2})}{{m}^{2}+1}$],根據對稱性可知D[$\frac{m(1-{m}^{2})}{{m}^{2}+1}$,$\frac{1-{m}^{2}}{m({m}^{2}+1)}$],
如圖,設A′B′交x軸于F,交y軸于E,連接AA′,作DN⊥OF于N,CM⊥OE于M,DN交CM于G.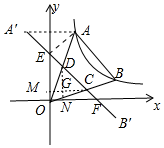
∵OE=OF=$\frac{1}{m}$-m,
∴∠OEF=∠OFE=45°,
∴∠A′EA=90°,AE=$\sqrt{2}$m,
在Rt△CDG中,∵DG=CG,CD=$\sqrt{2}$CG=$\sqrt{2}$[$\frac{1-{m}^{2}}{m({m}^{2}+1)}$-$\frac{m(1-{m}^{2})}{{m}^{2}+1}$].
同理可得,AB=$\sqrt{2}$($\frac{1}{m}$-m),
∵四邊形ADCB的面積為$\frac{6}{5}$,
∴$\frac{\sqrt{2}(\frac{1}{m}-m)+\sqrt{2}[\frac{1-{m}^{2}}{m({m}^{2}+1)}-\frac{m(1-{m}^{2})}{{m}^{2}+1}]}{2}$•$\sqrt{2}$m=$\frac{6}{5}$,
整理得$\frac{2(1-{m}^{2})}{{m}^{2}+1}$=$\frac{6}{5}$,解得m2=$\frac{1}{4}$,∵m>0,
∴m=$\frac{1}{2}$,
∴A($\frac{1}{2}$,2),C($\frac{6}{5}$,$\frac{3}{10}$).
故答案為($\frac{1}{2}$,2)或($\frac{6}{5}$,$\frac{3}{10}$).
點評 本題考查反比例函數圖象上點的特征、一次函數函數的應用、軸對稱、等腰直角三角形的判定和性質等知識,解題的關鍵是學會利用參數解決問題,學會構建一次函數,利用方程組確定直線的交點坐標,屬于中考填空題中的壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,A,B是直線l上的兩點,AB=4厘米,過l外一點C作CD∥l,射線BC與l所組成的銳角為60°,線段BC=2厘米,動點P、Q分別從B、C同時出發,P以1厘米/秒的速度,沿由B向C的方向運動;Q以2厘米/秒的速度,沿由C向D的方向運動,設P、Q運動的時間為t秒,當t>2時,PA交CD于點E.
如圖,A,B是直線l上的兩點,AB=4厘米,過l外一點C作CD∥l,射線BC與l所組成的銳角為60°,線段BC=2厘米,動點P、Q分別從B、C同時出發,P以1厘米/秒的速度,沿由B向C的方向運動;Q以2厘米/秒的速度,沿由C向D的方向運動,設P、Q運動的時間為t秒,當t>2時,PA交CD于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,從以下四個條件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.
如圖,從以下四個條件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
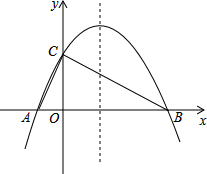 如圖,已知拋物線y=-$\frac{1}{4}$x2+bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為A(-2,0).
如圖,已知拋物線y=-$\frac{1}{4}$x2+bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為A(-2,0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在四邊形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,則四邊形ABCD的面積為=31,BD的長為2$\sqrt{41}$.
如圖,在四邊形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,則四邊形ABCD的面積為=31,BD的長為2$\sqrt{41}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com