
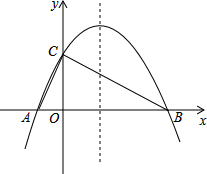
 如圖,已知拋物線y=-$\frac{1}{4}$x2+bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為A(-2,0).
如圖,已知拋物線y=-$\frac{1}{4}$x2+bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為A(-2,0).分析 (1)把A點坐標代入拋物線解析式可求得b的值,則可求得拋物線解析式及其對稱軸方程;
(2)由拋物線解析式可求得A、B、C的坐標,根據待定系數法可求得直線BC的解析式;
(3)由A、B、C的坐標可求得OA、OC、OB的長,根據相似三角形的判定可證明△AOC∽△COB.
解答 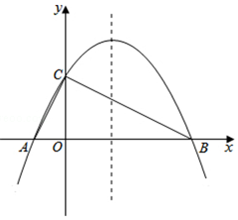 解:
解:
(1)∵拋物線y=-$\frac{1}{4}$x2+bx+4的圖象經過點A(-2,0),
∴-$\frac{1}{4}$×(-2)2+b×(-2)+4=0,解得b=$\frac{3}{2}$,
∴拋物線解析式為 y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
又∵y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{4}$(x-3)2+$\frac{25}{4}$,
∴對稱軸方程為x=3;
(2)在y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4中,令x=0,得y=4,
∴C(0,4),
令y=0,即-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0,整理得x2-6x-16=0,解得x=8或x=-2,
∴A(-2,0),B(8,0),
設直線BC的解析式為y=kx+b,
把B(8,0),C(0,4)的坐標分別代入解析式$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直線BC的解析式為y=-$\frac{1}{2}$x+4;
(3)△AOC∽△COB成立.
理由如下:
在△AOC與△COD中,
∵OA=2,OC=4,OB=8,
∴$\frac{OA}{OC}$=$\frac{OC}{OB}$,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB.
點評 本題為一次函數的綜合應用,涉及待定系數法、二次函數的性質、一元二次方程及相似三角形的判定等知識.在(1)中掌握函數圖象上的點的坐標滿足函數解析式是解題的關鍵,在(2)中求得B、C的坐標是解題的關鍵,在(3)中分別求得OA、OC、OB的長是解題的關鍵.本題考查知識點較多,綜合性較強,但難度不大.


科目:初中數學 來源: 題型:解答題
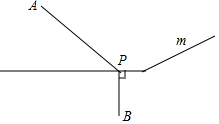 如圖所示,在兩個村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現要在河邊修一個水泵站,同時向A,B兩村供水,為了節約建設的費用,就要使所鋪設的管道最短,某人甲提出了這樣的建議:從點B向河道作垂線交m于點P,則點P為水泵站的位置.
如圖所示,在兩個村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現要在河邊修一個水泵站,同時向A,B兩村供水,為了節約建設的費用,就要使所鋪設的管道最短,某人甲提出了這樣的建議:從點B向河道作垂線交m于點P,則點P為水泵站的位置.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
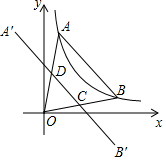 如圖,點A、B在函數y=$\frac{1}{x}$(x>0)的圖象上,點A在點B的左側,且OA=OB,點A關于y軸的對稱點為A′,點B關于x軸的對稱點為B′,連接A′B′分別交OA、OB于點D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點A的坐標為($\frac{1}{2}$,2),點C的坐標為($\frac{6}{5}$,$\frac{3}{10}$).
如圖,點A、B在函數y=$\frac{1}{x}$(x>0)的圖象上,點A在點B的左側,且OA=OB,點A關于y軸的對稱點為A′,點B關于x軸的對稱點為B′,連接A′B′分別交OA、OB于點D、C.若四邊形ABCD的面積為$\frac{6}{5}$,則點A的坐標為($\frac{1}{2}$,2),點C的坐標為($\frac{6}{5}$,$\frac{3}{10}$).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 組別 | 成績(分) | 頻數(人數) | 頻率 |
| 第1組 | 5 | 4 | a |
| 第2組 | 6 | 5 | 0.125 |
| 第3組 | 7 | b | 0.15 |
| 第4組 | 8 | 12 | 0.25 |
| 第5組 | 9 | 8 | 0.2 |
| 第6組 | 10 | 5 | 0.125 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com