
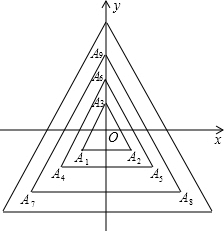
 如圖,所有正三角形的一邊平行于x軸,一頂點在y軸上,從內到外,它們的邊長依次為2,4,6,8,…,頂點依次用A1、A2、A3、A4、…表示,其中A1A2與x軸、底邊A1A2與A4A5、A4A5與A7A8、…均相距一個單位,則A2017的坐標是(-673,-673).
如圖,所有正三角形的一邊平行于x軸,一頂點在y軸上,從內到外,它們的邊長依次為2,4,6,8,…,頂點依次用A1、A2、A3、A4、…表示,其中A1A2與x軸、底邊A1A2與A4A5、A4A5與A7A8、…均相距一個單位,則A2017的坐標是(-673,-673). 分析 先根據每一個三角形有三個頂點確定出A2017所在的三角形,再求出相應的三角形的邊長以及A2017的縱坐標的長度,即可得解.
解答 解:∵2017÷3=672…1,
∴A2017是第673個等邊三角形的第1個頂點,
第673個等邊三角形邊長為2×673=1346,
∴點A2017的橫坐標為 $\frac{1}{2}$×(-1346)=-673,
∵邊A1A2與A4A5、A4A5與A7A8、…均相距一個單位,
∴點A2017的縱坐標為-673,
∴點A2014的坐標為(-673,-673),
故答案為:(-673,-673).
點評 本題考查了點的坐標、等邊三角形的性質,是點的變化規律,主要利用了等邊三角形的性質,確定出點A2017所在三角形是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
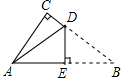 如圖是一張直角三角形的紙片,兩直角邊AC=6cm、BC=8cm,現將△ABC折疊,使點B與點A重合,折痕為DE,則BE的長為( )
如圖是一張直角三角形的紙片,兩直角邊AC=6cm、BC=8cm,現將△ABC折疊,使點B與點A重合,折痕為DE,則BE的長為( )| A. | 4 cm | B. | 5 cm | C. | 6 cm | D. | 10 cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正△ABC的邊長為2,以BC邊上的高AB1為邊作正△AB1C1,△ABC與△AB1C1公共部分的面積記為S1;再以正△AB1C1邊B1C1上的高AB2為邊作正△AB2C2,△AB1C1與△AB2C2公共部分的面積記為S2;…,以此類推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,則Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如圖,正△ABC的邊長為2,以BC邊上的高AB1為邊作正△AB1C1,△ABC與△AB1C1公共部分的面積記為S1;再以正△AB1C1邊B1C1上的高AB2為邊作正△AB2C2,△AB1C1與△AB2C2公共部分的面積記為S2;…,以此類推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,則Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.
初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
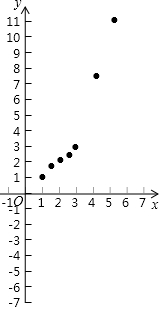 有這樣一個問題:探究函數y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性質.
有這樣一個問題:探究函數y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性質.| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com