
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
分析 從拋物線與x軸最多一個(gè)交點(diǎn)及a<b<0,可以推斷拋物線有最大值為0,對(duì)稱軸在y軸左側(cè),并得到b2-4ac≤0,從而得到①②為正確,③錯(cuò)誤;利用函數(shù)y=函數(shù)y=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,根據(jù)函數(shù)的最值問題即可解決.④正確.
解答 解:∵a<b<0
∴-$\frac{b}{2a}$<0,拋物線有最大值為0,
∴c<0;該拋物線的對(duì)稱軸在y軸左側(cè);
所以①正確;②正確;
∵拋物線與x軸最多有一個(gè)交點(diǎn),
∴b2-4ac≤0,
∴關(guān)于x的方程ax2+bx+c+2=0中,△=b2-4a(c+2)=b2-4ac-8a,
∵a<0,
∴-8a>0,
當(dāng)|b2-4ac|≥|8a|,則關(guān)于x的方程ax2+bx+c+2=0有實(shí)數(shù)根,
當(dāng)|b2-4ac|<|8a|,則關(guān)于x的方程ax2+bx+c+2=0無實(shí)數(shù)根,
∴關(guān)于x的方程ax2+bx+c+2=0的根的情況不確定;
所以③錯(cuò)誤;
∵函數(shù)y=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,
∵$\frac{a}{b}$>0,
∴函數(shù)y有最小值-$\frac{b}{4a}$,
∴$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$.所以④正確.
故選:B.
點(diǎn)評(píng) 本題考查了二次函數(shù)的解析式與圖象的關(guān)系,解答此題的關(guān)鍵是要明確a的符號(hào)決定了拋物線開口方向;a、b的符號(hào)決定對(duì)稱軸的位置;拋物線與x軸的交點(diǎn)個(gè)數(shù),決定了b2-4ac的符號(hào).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個(gè) | B. | 3個(gè) | C. | 4個(gè) | D. | 5個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 方程 3x-2=2x+1,移項(xiàng),得 3x-2x=-1+2 | |
| B. | 方程 3-x=2-5(x-1),去括號(hào),得 3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}$x=$\frac{3}{2}$,未知數(shù)系數(shù)化為 1,得 x=1 | |
| D. | 方程$\frac{x-1}{2}$-$\frac{x}{5}$=1 化成 5(x-1)-2x=10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
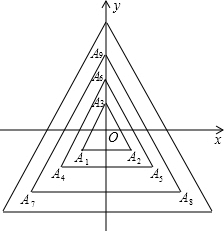 如圖,所有正三角形的一邊平行于x軸,一頂點(diǎn)在y軸上,從內(nèi)到外,它們的邊長(zhǎng)依次為2,4,6,8,…,頂點(diǎn)依次用A1、A2、A3、A4、…表示,其中A1A2與x軸、底邊A1A2與A4A5、A4A5與A7A8、…均相距一個(gè)單位,則A2017的坐標(biāo)是(-673,-673).
如圖,所有正三角形的一邊平行于x軸,一頂點(diǎn)在y軸上,從內(nèi)到外,它們的邊長(zhǎng)依次為2,4,6,8,…,頂點(diǎn)依次用A1、A2、A3、A4、…表示,其中A1A2與x軸、底邊A1A2與A4A5、A4A5與A7A8、…均相距一個(gè)單位,則A2017的坐標(biāo)是(-673,-673).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com