
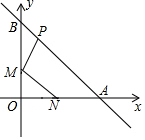
 如圖所示,已知點N(1,0),直線y=-x+2與兩坐標軸分別交于A,B兩點,M,P分別是線段OB,AB上的動點,則PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.
如圖所示,已知點N(1,0),直線y=-x+2與兩坐標軸分別交于A,B兩點,M,P分別是線段OB,AB上的動點,則PM+MN的最小值是$\frac{3\sqrt{2}}{2}$. 分析 如圖,點N關于OB的對稱點N′(-1,0),過點N′作N′P⊥AB交OB于M,則PN′=PM+MN的最小值,根據直線AB的解析式為y=-x+2,得到直線N′P的解析式為y=x+1,得到P($\frac{1}{2}$,$\frac{3}{2}$),推出△PAN′是等腰直角三角形,于是得到結論.
解答 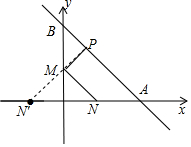 解:如圖,點N關于OB的對稱點N′(-1,0),過點N′作N′P⊥AB交OB于M,
解:如圖,點N關于OB的對稱點N′(-1,0),過點N′作N′P⊥AB交OB于M,
則PN′=PM+MN的最小值,
∵直線AB的解析式為y=-x+2,
∴直線N′P的解析式為y=x+1,
由$\left\{\begin{array}{l}{y=-x+2}\\{y=x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴P($\frac{1}{2}$,$\frac{3}{2}$),
∵A(2,0),B(0,2),
∴OA=OB,
∴∠BAO=45°,
∴△PAN′是等腰直角三角形,
∵AN′=3,
∴PN′=$\frac{3\sqrt{2}}{2}$,
∴PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.
故答案為$\frac{3\sqrt{2}}{2}$.
點評 本題考查軸對稱-最短問題、兩點之間距離公式等知識,解題的關鍵是利用對稱性找到點D、點E位置,屬于中考常考題型.


 優學名師名題系列答案
優學名師名題系列答案科目:初中數學 來源: 題型:填空題
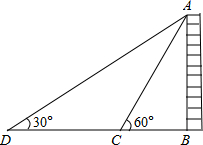 如圖,為測量某棟樓房AB的高度,在C點測得A點的仰角為30°,朝樓房AB方向前進10米到達點D,再次測得A點的仰角為60°,則此樓房的高度為5$\sqrt{3}$米(結果保留根號).
如圖,為測量某棟樓房AB的高度,在C點測得A點的仰角為30°,朝樓房AB方向前進10米到達點D,再次測得A點的仰角為60°,則此樓房的高度為5$\sqrt{3}$米(結果保留根號).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
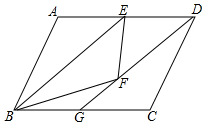 如圖,?ABCD中,E為AD邊的中點,把△ABE沿BE翻折,得到△FBE,連接DF并延長交BC于G.
如圖,?ABCD中,E為AD邊的中點,把△ABE沿BE翻折,得到△FBE,連接DF并延長交BC于G.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
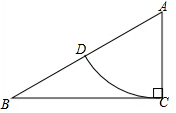 如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結果保留π)
如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結果保留π)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com