
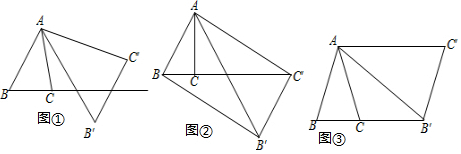
分析 (1)根據(jù)變換[60°,$\sqrt{3}$]的定義,即可解決問題.
(2)想辦法求出∠CAC′,以及$\frac{AC′}{AC}$的值即可.
(3)想辦法求出∠BAB′,以及$\frac{B′C′}{BC}$的值即可
解答 解:(1)如圖①中,設(shè)直線BC與直線B′C′的交點為H,AB′交BH于O.
∵△ABC∽△AB′C′,
AB:AB′=$\sqrt{3}$,
∴S△ABC:S△AB′C′=3,
∵∠B=∠B′,∠AOB=∠HOB′,
∴∠OHB=∠BAO=60°,
故答案為3,60°.
(2)如圖②中,
∵四邊形ABB′C′是矩形,
∴∠BAC′=90°.
∴θ=∠CAC′=∠BAC′-∠BAC=90°-30°=60°.
在Rt△ABB′中,∠ABB′=90°,∠BAB′=60°,
∴n=$\frac{AB′}{AB}$=2.
(3)如圖③中,
∵四邊形ABB′C′是平行四邊形,∴AC′∥BB′,
又∵∠BAC=36°,
∴θ=∠CAC′=∠ACB=72°
∴∠C′AB′=∠ABB′=∠BAC=36°,
∴θ=∠BAB′=72°,
又∵∠B=∠B,
∴△ABC∽△B′BA,
∴AB2=CB•B′B=CB•(BC+CB′),
∵CB′=AC=AB=B′C′,BC=1,
∴AB2=1•(1+AB)
∴AB=$\frac{1±\sqrt{5}}{2}$,
∵AB>0,
∴n=$\frac{B′C′}{BC}$=$\frac{1+\sqrt{5}}{2}$.
點評 本題考查四邊形綜合題、相似三角形的性質(zhì)、一元二次方程、變換[θ,n]的定義等知識,解題的關(guān)鍵是理解題意,靈活運用所學知識解決問題,屬于中考常考題型.


科目:初中數(shù)學 來源: 題型:填空題
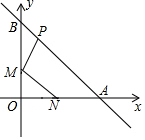 如圖所示,已知點N(1,0),直線y=-x+2與兩坐標軸分別交于A,B兩點,M,P分別是線段OB,AB上的動點,則PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.
如圖所示,已知點N(1,0),直線y=-x+2與兩坐標軸分別交于A,B兩點,M,P分別是線段OB,AB上的動點,則PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
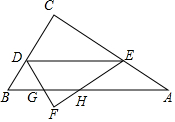 直角三角形ABC中,∠C=90度,CB=6,AC=8,D為CB邊上一個動點,E為AC上一點,DE∥AB,將三角形CDE沿著DE翻折得到三角形DEF,設(shè)三角形DEF和三角形ABC重合的面積為y,DC=x,求y與x的函數(shù)關(guān)系式及定義域.
直角三角形ABC中,∠C=90度,CB=6,AC=8,D為CB邊上一個動點,E為AC上一點,DE∥AB,將三角形CDE沿著DE翻折得到三角形DEF,設(shè)三角形DEF和三角形ABC重合的面積為y,DC=x,求y與x的函數(shù)關(guān)系式及定義域.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com