
分析 (1)用P(a,b)表示△OAB內的格點,a,b為正整數,假設結論不成立,則點P位于某條線段OCi內部.如圖,過點P作PE⊥OB于點E,過點Ci作CiF⊥AB于點F.
由△OEP∽△OFCi,知$\frac{b}{a}$=$\frac{p-i}{i}$,得到i≤a,這與a<i矛盾.得到原結論成立.
(2)假設結論不成立,即p為質數,故p=xy,其中x,y∈N,且2≤x,y≤p-1,因為△OAB內部的格點的橫、縱坐標之和可以是從2到p-1之間的任何整數,故必存在一格點P(a,b)滿足a+b=x,得到點P(a,b)在線段OCi內部,即在線段OC上除端點外還有其它格點,這與已知矛盾.得到原結論成立.
解答 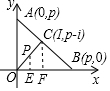 解:(1)用P(a,b)表示△OAB內的格點,a,b為正整數,
解:(1)用P(a,b)表示△OAB內的格點,a,b為正整數,
假設結論不成立,則點P位于某條線段OCi內部.
如圖,過點P作PE⊥OB于點E,過點Ci作CiF⊥AB于點F.
由△OEP∽△OFCi,知$\frac{b}{a}$=$\frac{p-i}{i}$,
其中1≤i≤p-1,
則1≤a≤i,1≤b≤p-i,
由$\frac{b}{a}$=$\frac{p-i}{i}$,知(a+b)i=ap,
則i|ap,
因為p為質數,且1≤i≤p-1,
則i與p互質,
則i|a,
故i≤a,
這與a<i矛盾.
所以,假設不成立,
所以原結論成立.
(2)假設結論不成立,即p為質數,故p=xy,其中x,y∈N,且2≤x,y≤p-1,
因為△OAB內部的格點的橫、縱坐標之和可以是從2到p-1之間的任何整數,
故必存在一格點P(a,b)滿足a+b=x,
則(a+b)y=xy=p,即ay+by=p,
故點(ay,by)必是C1(1,p-1),…,Ci(i,p-i),…,Cp-1(p-1,1)中的一個點,
設為Ci(i,p-i),
則有ya=i,by=p-i,
故$\frac{b}{a}$=$\frac{p-i}{i}$,
所以點P(a,b)在線段OCi內部,即在線段OC上除端點外還有其它格點,這與已知矛盾.
故原結論成立.
點評 此題考查了質數與合數,是競賽題型,難度較大,本題關鍵是通過假設法,得到矛盾的結論,從而求解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
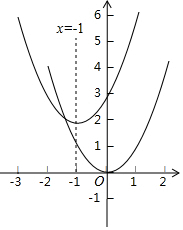 在學完《二次函數》后,老師給小明布置了家庭作業:完成下列表格,再用描點法在同一坐標系中畫出y1與y2的函數圖象.
在學完《二次函數》后,老師給小明布置了家庭作業:完成下列表格,再用描點法在同一坐標系中畫出y1與y2的函數圖象.| x | … | 0 | 1 | 2 |
| y1=ax2 | … | 0 | 1 | 4 |
| y2=ax2+bx+c | … | 3 | 6 | 11 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com