
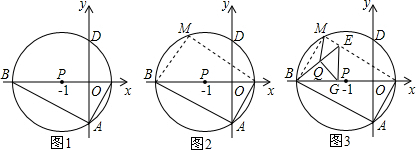
分析 (1)連接PA,運用垂徑定理及勾股定理即可求出圓的半徑,從而可以求出B、C兩點的坐標.
(2)由于圓P是中心對稱圖形,顯然射線AP與圓P的交點就是所需畫的點M,連接MB、MC即可;易證四邊形ACMB是矩形;過點M作MH⊥BC,垂足為H,易證△MHP≌△AOP,從而求出MH、OH的長,進而得到點M的坐標.
(3)易證點E、M、B、G在以點Q為圓心,QB為半徑的圓上,從而得到∠MQG=2∠MBG.由直角三角形和等邊三角形的性質得出∠PCA=60°,從而得到∠MBG=60°,進而得到∠MQG=120°,即∠MQG的度數是定值.
解答 解:(1)連接PA,如圖1所示.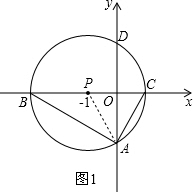
∵PO⊥AD,
∴AO=DO.
∵AD=2$\sqrt{3}$,
∴OA=$\sqrt{3}$.
∵點P坐標為(-1,0),
∴OP=1.
∴PA=$\sqrt{O{P}^{2}+O{A}^{2}}$=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴BP=CP=2,
∴OB=2+1=3,OC=2-1=1.
∴B(-3,0),C(1,0).
(2)連接AP,延長AP交⊙P于點M,連接MB、MC.
如圖2所示,線段MB、MC即為所求作.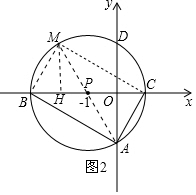
四邊形ACMB是矩形.理由如下:
∵△MCB由△ABC繞點P旋轉180°所得,
∴四邊形ACMB是平行四邊形.
∵BC是⊙P的直徑,
∴∠CAB=90°.
∴平行四邊形ACMB是矩形.
過點M作MH⊥BC,垂足為H,如圖2所示.
在△MHP和△AOP中,
∵$\left\{\begin{array}{l}{∠MHP=∠AOP}\\{∠HPM=∠OPA}\\{PM=PM}\end{array}\right.$,
∴△MHP≌△AOP(AAS).
∴MH=OA=$\sqrt{2}$,PH=PO=1.
∴OH=2.
∴點M的坐標為(-2,$\sqrt{2}$).
(3)在旋轉過程中∠MQG的大小不變.
∵四邊形ACMB是矩形,
∴∠BMC=90°.
∵EG⊥BO,
∴∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵點Q是BE的中點,
∴QM=QE=QB=QG.
∴點E、M、B、G在以點Q為圓心,QB為半徑的圓上,如圖3所示.
∴∠MQG=2∠MBG.
∵OA=$\sqrt{3}$,OP=1,∠AOP=90°,
∴∠APC=60°,
∵PC=PA,
∴∠PCA=∠PAC=60°,
∴∠MBC=∠BCA=60°.
∴∠MQG=120°.
∴在旋轉過程中∠MQG的大小不變,始終等于120°.
點評 本題考查了垂徑定理、勾股定理、全等三角形的判定與性質、矩形的判定與性質、圓周角定理、等腰三角形的性質、三角形內角和定理、四點共圓、圖形的旋轉等知識,綜合性比較強.有一定難度,證明點E、M、B、G在以點Q為圓心,QB為半徑的圓上是解決第三小題的關鍵.


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\overrightarrow{b}$$∥\overrightarrow{a}$ | B. | |$\overrightarrow{b}$|=3|$\overrightarrow{a}$| | C. | $\overrightarrow{b}$與$\overrightarrow{a}$的方向相反 | D. | 3$\overrightarrow{a}$+$\overrightarrow{b}$=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
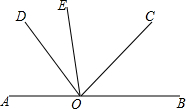 如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.
如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com