
 如圖,在圓O中,弦AB⊥CD于E,弦AG⊥BC于F,CD與AG相交于點M.
如圖,在圓O中,弦AB⊥CD于E,弦AG⊥BC于F,CD與AG相交于點M.分析 (1)連結AD、BD、BG,由AB⊥CD,AG⊥BC得到∠CEB=∠AFB=90°,根據等角的余角相等得到∠ECB=∠BAF,即可得出結論;
(2)連接OA、OB、OC、OG、CG,作OH⊥CG于H,OK⊥AB于K,由垂徑定理得出CH=GH=$\frac{1}{2}$CG,AK=BK=$\frac{1}{2}$AB=6,由圓周角定理和角的互余關系證出∠CNF=∠AGC,得出CG=CM=4,因此GH=2,由AG⊥BC證出$\widehat{BG}$的度數+$\widehat{AC}$的度數=180°,得出∠COG+∠AOB=180°,因此∠HOG+∠BOK=90°,證出∠HGO=∠BOK,由AAS證明△HOG≌△KBO,得出對應邊相等OK=HG=2,再由勾股定理求出OB即可.
解答 (1)證明:連結AD、BD、BG,如圖1所示,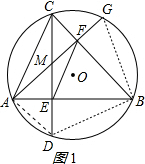
∵AB⊥CD,AG⊥BC,
∴∠CEB=∠AFB=90°,
∴∠ECB+∠B=90°,∠BAF+∠B=90°,
∴∠ECB=∠BAF,即∠DCB=∠BAG,
∴$\widehat{BD}$=$\widehat{BG}$;
(2)解:連接OA、OB、OC、OG、CG,作OH⊥CG于H,OK⊥AB于K,如圖2所示:
則CH=GH=$\frac{1}{2}$CG,AK=BK=$\frac{1}{2}$AB=6,
∵∠DCB=∠BAG,∠DCB+∠CMF=90°,∠BAG+∠ABF=90°,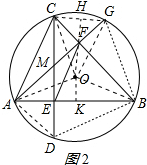
∴∠CMF=∠ABF,
∵∠ABF=∠AGC,
∴∠CMF=∠AGC,
∴CG=CM=4,
∴GH=2,
∵AG⊥BC,
∴∠AFB=90°,
∴∠FAB+∠FBA=90°,
∴$\widehat{BG}$的度數+$\widehat{AC}$的度數=180°,
∴∠COG+∠AOB=180°,
∴∠HOG+∠BOK=90°,
∵∠HGO+∠HOG=90°,
∴∠HGO=∠BOK,
在△HOG和△KBO中,$\left\{\begin{array}{l}{∠OHG=∠BKO=90°}\\{∠HGO=∠BOK}\\{OG=OB}\end{array}\right.$,
∴△HOG≌△KBO(AAS),
∴OK=HG=2,
∴OB=$\sqrt{O{K}^{2}+B{K}^{2}}$=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$;
即⊙O的半徑為2$\sqrt{10}$.
點評 本題考查了圓周角定理、垂徑定理、全等三角形的判定與性質、勾股定理等知識;本題綜合性強,難度較大,特別是(2)中,需要作多條輔助線證明三角形全等和運用勾股定理才能得出結果.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 一個商標圖案如圖4中陰影部分,在長方形ABCD中,AB=6cm,BC=4cm,以點A為圓心,AD為半徑作圓與BA的延長線相交于點F,則陰影部分的面積是( )
一個商標圖案如圖4中陰影部分,在長方形ABCD中,AB=6cm,BC=4cm,以點A為圓心,AD為半徑作圓與BA的延長線相交于點F,則陰影部分的面積是( )| A. | (4π+4)cm2 | B. | (4π+8)cm2 | C. | (8π+4)cm2 | D. | (4π-16)cm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
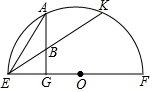 如圖,A是以EF為直徑的半圓上的一點,作AG⊥EF交EF于G,又B為AG上一點,EB的延長線交半圓于點K,若EB=2,EK=6,則AE=2$\sqrt{3}$.
如圖,A是以EF為直徑的半圓上的一點,作AG⊥EF交EF于G,又B為AG上一點,EB的延長線交半圓于點K,若EB=2,EK=6,則AE=2$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
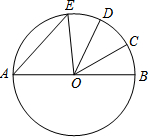 如圖,AB是⊙O的直徑,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,則∠AEO的度數是51°.
如圖,AB是⊙O的直徑,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,則∠AEO的度數是51°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com