
分析 (1)根據一元二次方程根的判別式即可得到結論;
(2)由于拋物線y=x2-mx+m-1過點(k-1,8)和點(-k+5,8).得到對稱軸為:x=$\frac{(k-1)(-k+5)}{2}$=2,求得m=4.得到結論;
(3)拋物線與x軸交與A、B(點A在點B的左邊),得到A(1,0),B(3,0),當M點在x軸的上方,當M點在x軸的下方,過M作ME⊥x軸于E,得到△MAB是等腰直角三角形,列方程得到結論.
解答 (1)證明:在x2-mx+m-1=0中,△=m2-4(m-1)=m2-4m+4=(m-2)2
∵當m取任何值時,(m-2)2≥0,
∴無論m取任何實數時,方程總有實數根.
(2)解:①∵拋物線y=x2-mx+m-1過點(k-1,8)和點(-k+5,8).
∴拋物線y=x2-mx+m-1的對稱軸為:x=$\frac{(k-1)(-k+5)}{2}$=2,
∴x=$\frac{m}{2}$,解得m=4.
∴y=x2-4x+3;
(3)解:∵拋物線x2-4x+3與x軸交與A、B(點A在點B的左邊),
∴A(1,0),B(3,0),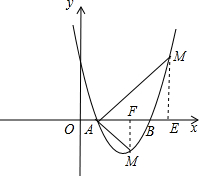
當M點在x軸的上方,
過M作ME⊥x軸于E,
∴△MAB是等腰直角三角形,
∴ME=AE,
即b=a-1,
∵M(a,b)為拋物線上任意一點,
∴a-1=a2-4a+3,
解得a=4,a=1(不合題意,舍去),
當M點在x軸的下方,
過M作MF⊥x軸于F,
∴△MAB是等腰直角三角形,
∴MF=AF,
即-b=a-1,
∵M(a,b)為拋物線上任意一點,
∴-a+1=a2-4a+3,
解得a=2,a=1(不合題意,舍去),
∴a的取值范圍為2≤a≤4.
點評 本題考查了二次方程的根的判別式以及拋物線的解析式求法,構建等腰直角三角形是本題的關鍵.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:選擇題
| A. | -$\sqrt{4}$ | B. | -$\frac{7}{11}$ | C. | $\sqrt{2}$ | D. | $\root{3}{-125}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
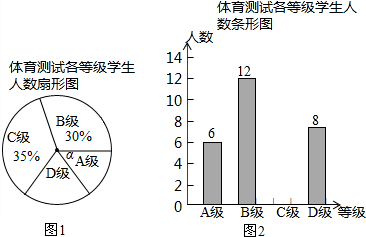
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
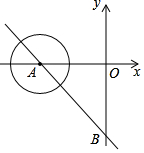 如圖,在直角坐標系中直線AB分別交x軸,y軸與A(-6,0)、B(0,-8)兩點,現有一半徑為1的動圓,圓心由A點,沿著AB方向以每秒1個單位的速度做平移運動,則經過幾秒后動圓與坐標軸相切.
如圖,在直角坐標系中直線AB分別交x軸,y軸與A(-6,0)、B(0,-8)兩點,現有一半徑為1的動圓,圓心由A點,沿著AB方向以每秒1個單位的速度做平移運動,則經過幾秒后動圓與坐標軸相切.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com