
分析 根據方程有實數根結合根的判別式即可得出關于k的一元一次不等式,解之即可得出k的取值范圍,設方程2x2+4x+3k=0的兩個根為x1、x2,根據根與系數的關系結合${{x}_{1}}^{2}+{{x}_{2}}^{2}$=7即可得出關于k的一元一次方程,解之即可得出k的值,結合k的取值范圍即可得出結論.
解答 解:∵方程2x2+4x+3k=0有實數根,
∴△=42-4×2×3k=16-24k≥0,
解得:k≤$\frac{2}{3}$.
設方程2x2+4x+3k=0的兩個根為x1、x2,
則有:x1+x2=-2,x1•x2=$\frac{3}{2}$k,
∵${{x}_{1}}^{2}+{{x}_{2}}^{2}$=7,
∴$({x}_{1}+{x}_{2})^{2}$-2x1•x2=4-3k=7,
解得:k=-1.
故k的值為-1.
點評 本題考查了根與系數的關系以及根的判別式,熟練掌握“x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$”是解題的關鍵.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
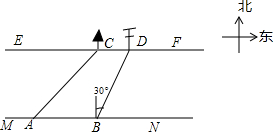 在綜合實踐課上,小聰所在小組要測量一條河的寬度,如圖,河岸EF∥MN,小聰在河岸MN上點A處測得河對岸小樹C位于東北方向,然后沿河岸走了30米,到達B處,測得河對岸電線桿D位于北偏東30°方向,此時,其他同學測得CD=10米.請根據這些數據求出河的寬度.(結果保留根號)
在綜合實踐課上,小聰所在小組要測量一條河的寬度,如圖,河岸EF∥MN,小聰在河岸MN上點A處測得河對岸小樹C位于東北方向,然后沿河岸走了30米,到達B處,測得河對岸電線桿D位于北偏東30°方向,此時,其他同學測得CD=10米.請根據這些數據求出河的寬度.(結果保留根號)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com