
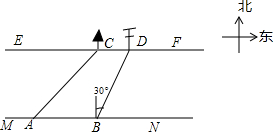
 在綜合實踐課上,小聰所在小組要測量一條河的寬度,如圖,河岸EF∥MN,小聰在河岸MN上點A處測得河對岸小樹C位于東北方向,然后沿河岸走了30米,到達B處,測得河對岸電線桿D位于北偏東30°方向,此時,其他同學測得CD=10米.請根據這些數據求出河的寬度.(結果保留根號)
在綜合實踐課上,小聰所在小組要測量一條河的寬度,如圖,河岸EF∥MN,小聰在河岸MN上點A處測得河對岸小樹C位于東北方向,然后沿河岸走了30米,到達B處,測得河對岸電線桿D位于北偏東30°方向,此時,其他同學測得CD=10米.請根據這些數據求出河的寬度.(結果保留根號) 分析 如圖作BH⊥EF,CK⊥MN,垂足分別為H、K,則四邊形BHCK是矩形,設CK=HB=x,根據tan30°=$\frac{HD}{BH}$列出方程即可解決問題.
解答 解:如圖作BH⊥EF,CK⊥MN,垂足分別為H、K,則四邊形BHCK是矩形,
設CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK-AB=x-30,
∴HD=x-30+10=x-20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°=$\frac{HD}{BH}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{x-20}{x}$,
解得x=30+10$\sqrt{3}$.
∴河的寬度為(30+10$\sqrt{3}$)米.
點評 本題考查解直角三角形的應用、方向角、三角函數等知識,解題的關鍵是添加輔助線構造直角三角形,學會利用三角函數的定義,列出方程解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
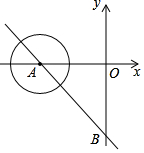 如圖,在直角坐標系中直線AB分別交x軸,y軸與A(-6,0)、B(0,-8)兩點,現有一半徑為1的動圓,圓心由A點,沿著AB方向以每秒1個單位的速度做平移運動,則經過幾秒后動圓與坐標軸相切.
如圖,在直角坐標系中直線AB分別交x軸,y軸與A(-6,0)、B(0,-8)兩點,現有一半徑為1的動圓,圓心由A點,沿著AB方向以每秒1個單位的速度做平移運動,則經過幾秒后動圓與坐標軸相切.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,O為坐標原點,點N的坐標為(20,0),點M在第一象限內,且OM=10,sin∠MON=$\frac{3}{5}$.求:
如圖,在平面直角坐標系中,O為坐標原點,點N的坐標為(20,0),點M在第一象限內,且OM=10,sin∠MON=$\frac{3}{5}$.求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com