
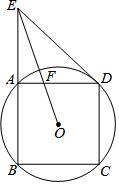
 如圖,正方形ABCD接于⊙O,延長(zhǎng)BA到E,使AE=AB,連接ED.
如圖,正方形ABCD接于⊙O,延長(zhǎng)BA到E,使AE=AB,連接ED.分析 (1)連接BD,則可知BD為直徑,根據(jù)正方形的性質(zhì)和已知條件可求得∠ADE=∠ODA=45°,可求得∠ODE=90°,可證得結(jié)論;
(2)由勾股定理可求得正方形的邊長(zhǎng),則可求得AE和AD,則可求得DE,在Rt△ODE中可求得OE的長(zhǎng),作OM⊥AB于M,根據(jù)平行線分線段成比例定理可證得EF=2OF,則可求得OF的長(zhǎng).
解答 (1)證明:如圖1,連接BD.
∵四邊形ABCD為正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直線ED是⊙O的切線;
(2)如圖2,作OM⊥AB于M,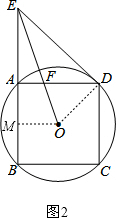
∵O為正方形的中心,
∴M為AB中點(diǎn),
∴AE=AB=2AM,AF∥OM,
∴$\frac{EF}{FO}$=$\frac{EA}{AM}$=2,
∴EF=2FO,
∵⊙O的半徑為2,
∴OD=2,BD=4,
∴AD=AE=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
∴DE=4,
在Rt△ODE中,由勾股定理可得OE=$\sqrt{O{D}^{2}+D{E}^{2}}$=2$\sqrt{5}$,
∴OF=$\frac{1}{3}$OE=$\frac{2\sqrt{5}}{3}$.
點(diǎn)評(píng) 本題主要考查切線的判定及正方形的性質(zhì),掌握切線的判定方法是解題的關(guān)鍵,注意兩種輔助線的作法,而在(2)中求得EF=2OF是解題的關(guān)鍵.


 導(dǎo)學(xué)與測(cè)試系列答案
導(dǎo)學(xué)與測(cè)試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,∠BAC=30°,AP平分∠BAC,GF垂直平分AP,交AC于F,Q為射線AB上一動(dòng)點(diǎn),若PQ的最小值為5,則AF的長(zhǎng)10.
如圖,∠BAC=30°,AP平分∠BAC,GF垂直平分AP,交AC于F,Q為射線AB上一動(dòng)點(diǎn),若PQ的最小值為5,則AF的長(zhǎng)10.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
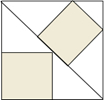 圖中有三個(gè)正方形,其中構(gòu)成的三角形中全等三角形的對(duì)數(shù)有( )
圖中有三個(gè)正方形,其中構(gòu)成的三角形中全等三角形的對(duì)數(shù)有( )| A. | 2對(duì) | B. | 3對(duì) | C. | 4對(duì) | D. | 5對(duì) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
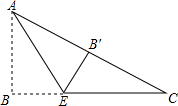 如圖,在Rt△ABC中,∠B=90°,∠C=30°,EC=4,將△ABC折疊,使點(diǎn)B恰好在邊AC上,與點(diǎn)B′重合,AE為折痕,則BE=2.
如圖,在Rt△ABC中,∠B=90°,∠C=30°,EC=4,將△ABC折疊,使點(diǎn)B恰好在邊AC上,與點(diǎn)B′重合,AE為折痕,則BE=2.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,在菱形ABCD中,對(duì)角線AC與BD相交于點(diǎn)O,OE⊥AB,垂足為E,若∠ADC=120°,則∠AOE=60°.
如圖,在菱形ABCD中,對(duì)角線AC與BD相交于點(diǎn)O,OE⊥AB,垂足為E,若∠ADC=120°,則∠AOE=60°.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖所示,小明家小區(qū)空地上有兩棵筆直的樹(shù)CD、EF.一天,他在A處測(cè)得樹(shù)頂D的仰角∠DAC=32°,在B處測(cè)得樹(shù)頂F的仰角∠FBE=45°,線段BF恰好經(jīng)過(guò)樹(shù)頂D.已知A、B兩處的距離為2米,兩棵樹(shù)之間的距離CE=3米,A、B、C、E四點(diǎn).在一條直線上,求樹(shù)EF的高度.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin32°=0.53,cos32°=0.85,tan32°=0.62.)
如圖所示,小明家小區(qū)空地上有兩棵筆直的樹(shù)CD、EF.一天,他在A處測(cè)得樹(shù)頂D的仰角∠DAC=32°,在B處測(cè)得樹(shù)頂F的仰角∠FBE=45°,線段BF恰好經(jīng)過(guò)樹(shù)頂D.已知A、B兩處的距離為2米,兩棵樹(shù)之間的距離CE=3米,A、B、C、E四點(diǎn).在一條直線上,求樹(shù)EF的高度.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin32°=0.53,cos32°=0.85,tan32°=0.62.)查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
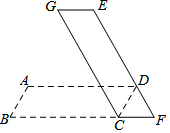 如圖,將平行四邊形ABCD繞點(diǎn)C順時(shí)針旋轉(zhuǎn)一定角度α(0°<α<180°)后,得到平行四邊形EFCG,若BC與CF在同一直線上,且點(diǎn)D恰好在EF上,則α=60°.
如圖,將平行四邊形ABCD繞點(diǎn)C順時(shí)針旋轉(zhuǎn)一定角度α(0°<α<180°)后,得到平行四邊形EFCG,若BC與CF在同一直線上,且點(diǎn)D恰好在EF上,則α=60°.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
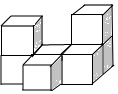 (1)用7個(gè)相同的小正方體拼了一個(gè)幾何體,畫出幾何體從左面和和上面看到的形狀圖;
(1)用7個(gè)相同的小正方體拼了一個(gè)幾何體,畫出幾何體從左面和和上面看到的形狀圖;查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com