
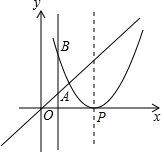
 己知拋物線y=(x-2)2,P是拋物線對稱軸上的一個點,直線x=t分別與直線y=x、拋物線交于點A,B,若△ABP是等腰直角三角形,則t的值為0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知拋物線y=(x-2)2,P是拋物線對稱軸上的一個點,直線x=t分別與直線y=x、拋物線交于點A,B,若△ABP是等腰直角三角形,則t的值為0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$. 分析 首先求出拋物線與直線y=x的交點坐標,再分四種情形列出方程即可解決問題.
解答 解:由$\left\{\begin{array}{l}{y=x}\\{y=(x-2)^{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
根據的通知解三角形的性質可知當AB=|Px-Ax|或AB=2|Px-Ax|時,△PAB可以是等腰直角三角形.
①當0<x≤1時,(t-2)2-t=2-t或(t-2)2-t=2(2-t),
解得t=2-$\sqrt{2}$或0,
②當1<t≤2時,t-(t-2)2=2-t或t-(t-2)2=2(2-t),
解得t=3-$\sqrt{3}$或$\frac{7-\sqrt{17}}{2}$,
③當2<t≤4時,t-(t-2)2=(t-2),或t-(t-2)2=2(t-2),
解得t=2+$\sqrt{2}$或3,
④當t>4時,(t-2)2-t=t-2或(t-2)2-t=2(t-2),
解得t=3+$\sqrt{3}$或$\frac{7+\sqrt{17}}{2}$,
綜上所述,滿足條件的t的值為0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
故答案為0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
點評 本題考查二次函數的性質、一次函數的應用、等腰直角三角形的性質、一元二次方程等知識,解題的關鍵是學會用轉化的思想思考問題,學會構建方程解決問題,屬于中考填空題中的壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2 個 | C. | 3 個 | D. | 4 個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 路程(千米) | 運費(元/噸.千米) | |||
| 甲倉庫 | 乙倉庫 | 甲倉庫 | 乙倉庫 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
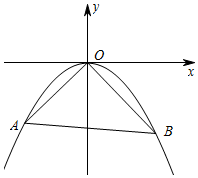 如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點A(x1,y1),B(x2,y2)兩點,拋物線y=ax2經過點(4,-2)
如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點A(x1,y1),B(x2,y2)兩點,拋物線y=ax2經過點(4,-2)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com