
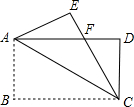
 如圖,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,請(qǐng)按照?qǐng)D中所標(biāo)注的數(shù)據(jù)計(jì)算圖中實(shí)線所圍成的圖形的面積S=50.
如圖,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,請(qǐng)按照?qǐng)D中所標(biāo)注的數(shù)據(jù)計(jì)算圖中實(shí)線所圍成的圖形的面積S=50. 分析 求出∠F=∠AGB=∠EAB=90°,∠FEA=∠BAG,根據(jù)AAS證△FEA≌△GAB,推出AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,求出FH=14,根據(jù)陰影部分的面積=S梯形EFHD-S△EFA-S△ABC-S△DHC和面積公式代入求出即可.
解答 解:∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中
∵$\left\{\begin{array}{l}{∠F=∠BGA}\\{∠FEA=∠BAG}\\{AE=AB}\end{array}\right.$,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面積是$\frac{1}{2}$×(EF+DH)×FH=$\frac{1}{2}$×(6+4)×14=70,
∴陰影部分的面積是S梯形EFHD-S△EFA-S△ABC-S△DHC
=70-$\frac{1}{2}$×6×2-$\frac{1}{2}$×(6+4)×2-$\frac{1}{2}$×4×2
=50.
故答案為50.
點(diǎn)評(píng) 本題考查了三角形的面積,梯形的面積,全等三角形的性質(zhì)和判定等知識(shí)點(diǎn),關(guān)鍵是把不規(guī)則圖形的面積轉(zhuǎn)化成規(guī)則圖形的面積.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 無實(shí)數(shù)根 | B. | 兩根之和為2 | C. | 兩根之積為-1 | D. | 有一個(gè)根為$1+\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 矩形的對(duì)角線相等 | |
| B. | 菱形的面積等于兩條對(duì)角線乘積的一半 | |
| C. | 對(duì)角線互相垂直的矩形是正方形 | |
| D. | 有兩個(gè)角相等的梯形是等腰梯形 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,將矩形ABCD沿對(duì)角線AC對(duì)折,使△ABC落在△ACE的位置,且CE與AD相交于點(diǎn)F,連結(jié)ED,若AB=$\sqrt{3}$,BC=3.
如圖,將矩形ABCD沿對(duì)角線AC對(duì)折,使△ABC落在△ACE的位置,且CE與AD相交于點(diǎn)F,連結(jié)ED,若AB=$\sqrt{3}$,BC=3.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 35 | B. | 350 | C. | 840 | D. | 2520 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
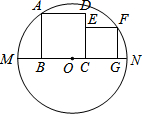 如圖,兩個(gè)正方形都在⊙O的直徑MN的同側(cè),頂點(diǎn)B、C、G都在MN上,正方形ABCD的頂點(diǎn)A和正方形CEFG的頂點(diǎn)F都在⊙O上,點(diǎn)E在CD上.若AB=5,F(xiàn)G=3,則OC的長(zhǎng)為2.
如圖,兩個(gè)正方形都在⊙O的直徑MN的同側(cè),頂點(diǎn)B、C、G都在MN上,正方形ABCD的頂點(diǎn)A和正方形CEFG的頂點(diǎn)F都在⊙O上,點(diǎn)E在CD上.若AB=5,F(xiàn)G=3,則OC的長(zhǎng)為2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
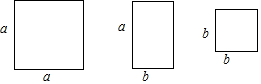
| A. | a+b | B. | 2a+b | C. | 2a-b | D. | a+2b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com