
分析 (1)利用已知將各分數分解,進而化簡求出答案;
(2)利用已知將各分數分解,進而化簡求出答案;
(3)結合(2)中所求,進而分解各數,即可得出答案.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$$+\frac{1}{4×5}$$+\frac{1}{5×6}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$
=1-$\frac{1}{6}$
=$\frac{5}{6}$;
故答案為:$\frac{5}{6}$;
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$;
故答案為:$\frac{n}{n+1}$;
(3)$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$=$\frac{1007}{2015}$,
解得:n=1007.
點評 此題主要考查了分式的加減運算,正確分解各數是解題關鍵.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別為A(-1,2),B(-3,4),C(-2,6).
如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別為A(-1,2),B(-3,4),C(-2,6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 要求:在下列空白處尺規作圖,保留作圖痕跡,不寫作法,要作答.
要求:在下列空白處尺規作圖,保留作圖痕跡,不寫作法,要作答.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知直線l1:y1=2x+3與直線l2:y2=kx-1交于A點,A點橫坐標為-1,且直線l1與x軸交于B點,與y軸交于D點,直線l2與y軸交于C點.
已知直線l1:y1=2x+3與直線l2:y2=kx-1交于A點,A點橫坐標為-1,且直線l1與x軸交于B點,與y軸交于D點,直線l2與y軸交于C點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
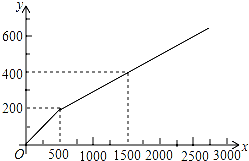 為加強與家長的溝通,某校在家長會到來之前需印刷《致家長的一封信》等材料以作宣傳,該校的印刷任務原來由甲復印店承接,其收費y(元)與印刷頁數x(頁)的函數關系如圖所示.
為加強與家長的溝通,某校在家長會到來之前需印刷《致家長的一封信》等材料以作宣傳,該校的印刷任務原來由甲復印店承接,其收費y(元)與印刷頁數x(頁)的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 觀察時間 | 10:30(t=0) | 10:36(t=6) | 10:48(t=18) |
| 路牌內容 | 上海90Km | 上海80Km | 上海60Km |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com