
 如圖,AB是⊙O的直徑,點P是弦AC上一動點(不與A,C重合),過點P作PD⊥AB,垂足為D,射線DP交$\widehat{AC}$于點E,交過點C的切線于點F.
如圖,AB是⊙O的直徑,點P是弦AC上一動點(不與A,C重合),過點P作PD⊥AB,垂足為D,射線DP交$\widehat{AC}$于點E,交過點C的切線于點F.分析 (1)連接OC,根據切線的性質得出OC⊥CF以及∠OAC=∠OCA得∠FCP=∠FPC,可證得結論;
(2)由∠CAB=30°易得△AOE、△EOC均是等邊三角形,可得AE=AO=OC=CE,易得以A,O,C,E為頂點的四邊形是菱形.
解答 (1)證明:連接OC
∵CF是⊙O的切線,
∴OC⊥CF,
∴∠FCA+∠ACO=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∵PD⊥AB,
∴∠PAD+∠APD=90°,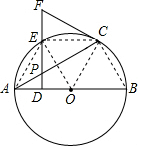
而∠APD=∠CPF,
∴∠PAD+∠CPF=90°,
∴∠FCP=∠FPC,
∴FC=FP;
(2)解:以A,O,C,E為頂點的四邊形是菱形,
理由如下:
∵∠CAB=30°,
∴∠ABC=60°,從而∠AOC=120°,
∵E是$\widehat{AC}$的中點,
∴∠AOE=∠EOC=60°,
∴△AOE、△EOC均是等邊三角形,
∴AE=AO=OC=CE,
∴四邊形AOCE是菱形.
點評 本題主要考查了切線的性質、圓周角定理和等邊三角形的判定等,作出恰當的輔助線利用切線的性質是解答此題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
 如圖,已知∠ABC=∠DCB,下列所給條件不能證明△ABC≌△DCB的是( )
如圖,已知∠ABC=∠DCB,下列所給條件不能證明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AC=BD | C. | ∠ACB=∠DBC | D. | AB=DC |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
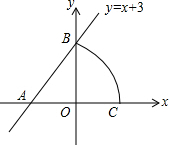 如圖,已知直線y=x+3與x軸交于點A,與y軸交于點B,以點A為圓心,AB為半徑畫弧,交x軸正半軸于點C,則點C坐標為( )
如圖,已知直線y=x+3與x軸交于點A,與y軸交于點B,以點A為圓心,AB為半徑畫弧,交x軸正半軸于點C,則點C坐標為( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
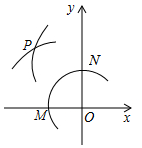 如圖,在平面直角坐標系中,以O為圓心,適當長為半徑畫弧,交x軸于點M,交y軸于點N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )
如圖,在平面直角坐標系中,以O為圓心,適當長為半徑畫弧,交x軸于點M,交y軸于點N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )| A. | a=b | B. | 2a-b=1 | C. | 2a+b=-1 | D. | 2a+b=1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com