
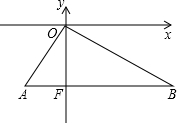
 如圖,在平面直角坐標系中,直角三角形的直角頂點與坐標原點重合,AB⊥y軸,垂足為點F,OA=2,∠B=30°,在Rt△OAB內(包含邊界)有一動點M(x,y),以M為圓心的⊙M經過原點O,且與AB邊相切于點C,⊙M與邊OA、OB分別交于點D、E,則DE的取值范圍為$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$.
如圖,在平面直角坐標系中,直角三角形的直角頂點與坐標原點重合,AB⊥y軸,垂足為點F,OA=2,∠B=30°,在Rt△OAB內(包含邊界)有一動點M(x,y),以M為圓心的⊙M經過原點O,且與AB邊相切于點C,⊙M與邊OA、OB分別交于點D、E,則DE的取值范圍為$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$. 分析 分別求出DE的最大值和最小值,如圖1中,當點M在OB上時,OM的值最大,設⊙M與AB相切于點G,OM=OG=r,由MG∥OF,推出$\frac{BM}{BO}$=$\frac{MG}{OF}$,可得$\frac{2\sqrt{3}-r}{2\sqrt{3}}$=$\frac{r}{\sqrt{3}}$,解得r=$\frac{2\sqrt{3}}{3}$,屬于DE的最大值為$\frac{4\sqrt{3}}{3}$.如圖2中,當點M在線段OF上時,切點為F,此時⊙M的半徑最小,OM=$\frac{1}{2}$OF=$\frac{\sqrt{3}}{2}$,所以DE的最大值為$\sqrt{3}$,由此即可解決問題.
解答 解:在Rt△AOB中,∵OA=2,∠B=30°,
∴AB=2OA=4,OB=$\sqrt{3}$OA=2$\sqrt{3}$,
OF=$\frac{1}{2}$OB=$\sqrt{3}$,BF=$\sqrt{3}$OF=3,
∵∠DOE=90°,
∴DE是⊙O的直徑,
∴DE=2OM.
如圖1中,當點M在OB上時,OM的值最大,設⊙M與AB相切于點G,OM=OG=r,
∵MG∥OF,
∴$\frac{BM}{BO}$=$\frac{MG}{OF}$,
∴$\frac{2\sqrt{3}-r}{2\sqrt{3}}$=$\frac{r}{\sqrt{3}}$,
∴r=$\frac{2\sqrt{3}}{3}$,
∴DE的最大值為$\frac{4\sqrt{3}}{3}$
如圖2中,當點M在線段OF上時,切點為F,此時⊙M的半徑最小,
OM=$\frac{1}{2}$OF=$\frac{\sqrt{3}}{2}$,所以DE的最大值為$\sqrt{3}$,
綜上所述,$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$.
點評 本題考查切線的性質、坐標與圖形的性質等知識,解題的關鍵是學會利用特殊位置解決DE的最大值以及最小值,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
 如圖,AB為⊙O的直徑,C為⊙O上一點,連AC、BC,E為⊙O上一點,且BE=CE,點F在BE上,CF⊥AB于D.
如圖,AB為⊙O的直徑,C為⊙O上一點,連AC、BC,E為⊙O上一點,且BE=CE,點F在BE上,CF⊥AB于D.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com