
(本題滿分10分)在一組數據 中,各數據與它們的平均數
中,各數據與它們的平均數 的差的絕對值的平均數,即
的差的絕對值的平均數,即 叫做這組數據的“平均差”. “平均差”也能描述一組數據的離散程度. “平均差”越大說明數據的離散程度越大.因為“平均差”的計算要比方差的計算要容易一點,所以有時人們也用它來代替方差來比較數據的離散程度.極差、方差(標準差)、平均差都是反映數據離散程度的量.
叫做這組數據的“平均差”. “平均差”也能描述一組數據的離散程度. “平均差”越大說明數據的離散程度越大.因為“平均差”的計算要比方差的計算要容易一點,所以有時人們也用它來代替方差來比較數據的離散程度.極差、方差(標準差)、平均差都是反映數據離散程度的量.
一水產養殖戶李大爺要了解魚塘中魚的重量的離散程度,因為個頭大小差異太大會出現“大魚吃小魚”的情況;為防止出現“大魚吃小魚”的情況,在能反映數據離散程度幾個的量中某些值超標時就要捕撈;分開養殖或出售;
他從兩個魚塘各隨機捕撈10條魚稱得重量如下:(單位:千克)
A魚塘:3、 5、 5、 5、 7、 7、 5、 5、 5、 3
B魚塘:4、 4、 5、 6、 6、 5、 6、 6、 4、 4
分別計算甲、乙兩個魚塘中抽取的樣本的極差、方差、平均差;完成下面的表格:
極差 | 方差 | 平均差 | |
A魚塘 | |||
B魚塘 |
(2)如果你是技術人員,你會建議李大爺注意哪個魚塘的風險更大些?計算哪些量更能說明魚重量的離散程度?
(1)(6分)
極差 | 方差 | 平均差 | |
A | 4 | 1.6 | 0.8 |
B | 2 | 0.8 | 0.8 |
(2)極差與方差 (4分)
【解析】
試題分析:(1)根據極差、方差、平均差的定義分別計算即可;(2)因為要防止出現“大魚吃小魚”的情況,所以注意了解魚塘中魚的重量的離散程度,即波動大小,波動大的風險更大,根據(1)中的數據可得極差與方差更能說明魚重量的離散程度.
試題解析:(1)甲組數據中最大的值7,最小值3,故極差=7-3=4,
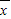 甲=(3×2+6×5+2×7)÷10=5,S2甲=
甲=(3×2+6×5+2×7)÷10=5,S2甲=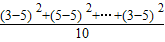 =1.6,
=1.6,
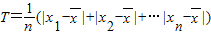 =
=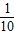 (|3-5|+|5-5|+…+|3-5|)=0.8;
(|3-5|+|5-5|+…+|3-5|)=0.8;
乙組數據中最大的值6,最小值4,故極差=6-4=2;乙=(4×4+6×4+5×2)÷10=5,
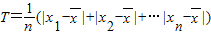 =
=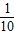 (|4-5|+|4-5|+…+|4-5|)=0.8;
(|4-5|+|4-5|+…+|4-5|)=0.8;
S2乙=[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2+(5-5)2+(6-5)2+(6-5)2+(4-5)2+(4-5)2]÷10=0.8,
極差 | 方差 | 平均差 | |
A | 4 | 1.6 | 0.8 |
B | 2 | 0.8 | 0.8 |
(2)∵S2甲<S2乙;所以根據A,B的極差與方差可以得出A魚塘風險更大.極差與方差更能說明魚重量的離散程度
考點:1. 極差;2. 方差;3. 平均差.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2014-2015學年安徽濉溪城關中心學校八年級上學期第三次月考數學卷(解析版) 題型:填空題
一次函數y=-3x+6的圖象與x軸的交點坐標是 ,與y軸的交點坐標是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校九年級上學期12月月考數學試卷(解析版) 題型:解答題
如圖,梯形ABCD中.AB∥CD.且AB=2CD,E,F分別是AB,BC的中點,EF與BD相交于點M.

(1)求證:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期第三次教學質量監測數學試卷(解析版) 題型:解答題
題滿分12分)在平面直角坐標系中,動點P到點S(1, ),與過T點(0,
),與過T點(0, )且平行于x軸的直線距離相等,設點P的坐標為(x,y)
)且平行于x軸的直線距離相等,設點P的坐標為(x,y)
(1)試求出y與x函數關系式;
(2)設點P運動到x軸上時為點A、B(點A在點B的左邊),運動到最高點為點C;動動到y軸上時為點D;求出A、B、C、D四點的坐標;
(3)在(2)的條件下, 為線段
為線段 (點O為坐標原點)上的一個動點,過
(點O為坐標原點)上的一個動點,過 軸上一點
軸上一點 作
作 的垂線,垂足為
的垂線,垂足為 ,直線
,直線 交
交 軸于點
軸于點 ,當
,當 點在線段
點在線段 上運動時,現給出兩個結論: ①
上運動時,現給出兩個結論: ①  ②
② ,其中有且只有一個結論是正確的,請你判斷哪個結論正確,并證明.
,其中有且只有一個結論是正確的,請你判斷哪個結論正確,并證明.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期第三次教學質量監測數學試卷(解析版) 題型:填空題
如圖,在直角梯形ABCD中,AD∥BC,∠B=90°,將直角梯形ABCD沿CE折疊,使點D落在AB上的F點,若AB=BC=12,EF=10, ∠FCD=90°,則AF=______.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊三校八年級上學期12月月考數學試卷(解析版) 題型:解答題
(10分)如圖,在平面直角坐標系中,Rt△ABC的三個頂點均在邊長為1的正方形網格格點上.
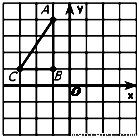
(1)作出△ABC關于y軸對稱的△A’B’C’;
(2)若點D在圖中所給的網格中的格點上,且以A、B、D為頂點的三角形為等腰直角三角形,請直接寫出點D的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com