
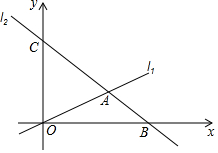
 如圖,在平面直角坐標系中,O為坐標原點,直線l1:y=$\frac{1}{2}$x與直線l2:y=-x+6交于點A,l2與x軸交于B,與y軸交于點C.
如圖,在平面直角坐標系中,O為坐標原點,直線l1:y=$\frac{1}{2}$x與直線l2:y=-x+6交于點A,l2與x軸交于B,與y軸交于點C.分析 (1)先根據直線解析式,求得C(0,6),再根據方程組的解,得出A(4,2),進而得到△OAC的面積;
(2)分兩種情況進行討論:①點M1在射線AC上,②點M2在射線AB上,分別根據點M的橫坐標,求得其縱坐標即可.
解答 解:(1)在y=-x+6中,令x=0,解得y=6,
∴C(0,6),即CO=6,
解方程組$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-x+6}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
∴A(4,2),
∴S△OAC=$\frac{1}{2}$×6×4=12;
(2)分兩種情況:
①如圖所示,當點M1在射線AC上時,過M1作M1D⊥CO于D,則△CDM1是等腰直角三角形,
∵A(4,2),C(0,6),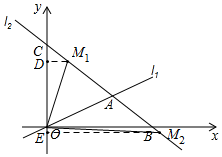
∴AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵△OAM的面積是△OAC面積的$\frac{3}{4}$,
∴AM1=$\frac{3}{4}$AC=3$\sqrt{2}$,
∴CM1=$\sqrt{3}$,
∴DM1=$\frac{\sqrt{6}}{2}$,即點M1的橫坐標為$\frac{\sqrt{6}}{2}$,
在直線y=-x+6中,當x=$\frac{\sqrt{6}}{2}$時,y=6-$\frac{\sqrt{6}}{2}$,
∴M1($\frac{\sqrt{6}}{2}$,6-$\frac{\sqrt{6}}{2}$);
②如圖所示,當點M2在射線AB上時,過M2作M2E⊥CO于E,則△CEM2是等腰直角三角形,
由題可得,AM2=AM1=3$\sqrt{2}$,
∴CM2=7$\sqrt{3}$,
∴EM2=$\frac{7}{2}\sqrt{6}$,即點M2的橫坐標為$\frac{7}{2}\sqrt{6}$,
在直線y=-x+6中,當x=$\frac{7}{2}\sqrt{6}$時,y=6-$\frac{7}{2}\sqrt{6}$,
∴M2($\frac{7}{2}\sqrt{6}$,6-$\frac{7}{2}\sqrt{6}$).
綜上所述,點M的坐標為($\frac{\sqrt{6}}{2}$,6-$\frac{\sqrt{6}}{2}$)或($\frac{7}{2}\sqrt{6}$,6-$\frac{7}{2}\sqrt{6}$).
點評 本題主要考查了兩直線相交的問題,解決問題的關鍵是掌握兩直線交點的坐標的計算方法,解題時注意:兩條直線的交點坐標,就是由這兩條直線相對應的一次函數表達式所組成的二元一次方程組的解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$和2 | B. | $\frac{3}{5}$和3 | C. | -$\frac{3}{5}$和2 | D. | -$\frac{3}{5}$和3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
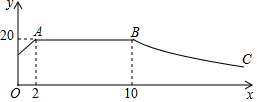 我市某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且大棚內溫度為20℃的條件下生長最快的新品種,如圖是某天恒溫系統從開啟到關閉及關閉后大棚內溫度y(單位:℃)隨光照時間x(單位:h)變化的大致圖象,其中BC段是雙曲線y=$\frac{k}{x}$的一部分.請根據圖中信息解答下列問題:
我市某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且大棚內溫度為20℃的條件下生長最快的新品種,如圖是某天恒溫系統從開啟到關閉及關閉后大棚內溫度y(單位:℃)隨光照時間x(單位:h)變化的大致圖象,其中BC段是雙曲線y=$\frac{k}{x}$的一部分.請根據圖中信息解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com