
 如圖,四邊形ABCD是正方形,以B點為圓心,BD的長為半徑畫弧交BC延長線于點E,以DE為邊作正方形DEFG,作FH⊥BE交BE的延長線于點H,連接AE、CG,則下列結論中正確的有( )
如圖,四邊形ABCD是正方形,以B點為圓心,BD的長為半徑畫弧交BC延長線于點E,以DE為邊作正方形DEFG,作FH⊥BE交BE的延長線于點H,連接AE、CG,則下列結論中正確的有( )| A. | ①②③④⑤ | B. | ①②③④ | C. | ①②③ | D. | ①②③⑤ |
分析 ①正確.根據等腰三角形的性質求出∠BDE=67.5°,再根據∠BDC=45°,即可解決問題.
②正確.首先證明△DCE≌△EHF,推出CE=FH,在Rt△EDC中,由DE2-DC2=CE2,可得S正方形DEFG-S正方形ABCD=FH2.
③正確.先證明△ADE≌△CDG,推出∠AED=∠DGC,由∠DGO+∠DOG=90°,∠DOG=∠POE,推出∠OEP+∠POE=90°,推出∠OPE=90°.
④錯誤.由AD∥CE,推出S△ACE=S△DCE,推出$\frac{1}{2}$•AE•CP=$\frac{1}{2}$•CD•CE,推出AE•CP=CD•CE,推出CG•CP=CD•CE,由CD>CE,推出CD•CE<CD2,推出CG•CP<CD2,即可證明.
⑤正確.如圖2中,在CD上取一點F,使得DF=EF,連接EF.由∠FDE=∠FED=22.5°,推出∠CFE=∠FDE+∠FED=45°,由∠ECF=90°,推出∠CFE=∠CEF=45°,推出CF=CE,設CF=CE=a,則EF=DF=$\sqrt{2}$a,根據S△CDE:S△BCD=$\frac{1}{2}$•a•(1+$\sqrt{2}$)a:$\frac{1}{2}$[(1+$\sqrt{2}$)a]2計算即可解決問題.
解答 解:如圖1中,設CG交DE于O,連接AC.
∵四邊形ABCD是正方形,
∴∠DBC=BDC=45°,
∵BD=BE,
∴∠BDE=∠BED=$\frac{180°-45°}{2}$=67.5°,
∴∠CDE=∠BDE-∠BDC=22.5°,故①正確,
∵FH⊥CH,四邊形DEFG是正方形,
∴∠DCE=∠EHF=∠DEF=90°,DE=EF,
∴∠DEC+∠FEH=90°,∠FEH+∠EFH=90°,
∴∠DEC=∠EFH,
在△DCE和△EHF中,
$\left\{\begin{array}{l}{∠DCE=∠EHF}\\{∠DEC=∠EFH}\\{DE=EF}\end{array}\right.$,
∴△DCE≌△EHF,
∴CE=FH,
在Rt△EDC中,∵DE2-DC2=CE2,
∴S正方形DEFG-S正方形ABCD=FH2,故②正確,
∵∠ADC=∠GDE=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDG}\\{DE=DG}\end{array}\right.$,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠DGC,
∵∠DGO+∠DOG=90°,∠DOG=∠POE,
∴∠OEP+∠POE=90°,
∴∠OPE=90°,
∴AE⊥CG,故③正確,
∵AD∥CE,
∴S△ACE=S△DCE,
∴$\frac{1}{2}$•AE•CP=$\frac{1}{2}$•CD•CE,
∴AE•CP=CD•CE,
∴CG•CP=CD•CE,
∵CD>CE,
∴CD•CE<CD2,
∴CG•CP<CD2,故④錯誤,
如圖2中,在CD上取一點F,使得DF=EF,連接EF.
∵∠FDE=∠FED=22.5°,
∴∠CFE=∠FDE+∠FED=45°,∵∠ECF=90°,
∴∠CFE=∠CEF=45°,
∴CF=CE,設CF=CE=a,則EF=DF=$\sqrt{2}$a,
∴S△CDE:S△BCD=$\frac{1}{2}$•a•(1+$\sqrt{2}$)a:$\frac{1}{2}$[(1+$\sqrt{2}$)a]2=$\sqrt{2}$-1,故⑤正確.
故選D.
點評 本題考查正方形的性質、相似三角形的判定和性質、全等三角形的判定和性質、等腰三角形的性質、勾股定理等知識,解題的關鍵是靈活運用所學知識解決問題,學會利用面積法解決線段之間的關系問題,學會用轉化的思想思考問題,屬于中考選擇題中的壓軸題.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
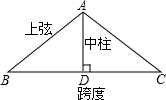 如圖,廠房屋頂人字架(等腰三角形)的跨度為20m,∠B=37°,求中柱AD(D為底邊中點)和上弦AB的長(參考數據:cos37°≈0.6)
如圖,廠房屋頂人字架(等腰三角形)的跨度為20m,∠B=37°,求中柱AD(D為底邊中點)和上弦AB的長(參考數據:cos37°≈0.6)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 甲 | 80 | 75 | 90 | 64 | 88 | 95 |
| 乙 | 84 | 80 | 88 | 76 | 79 | 85 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com