

分析 (1)根據對頂角相等求∠2,根據兩直線平行,同位角相等求∠3;
(2)①過點P作MN∥AB,根據平行線的性質得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性質易得∠EPF=∠PEB+∠PFD.
②同①;
③利用平行線的性質和三角形的外角性質得到三個角之間的關系.
解答 解:(1)∵∠2=∠1,∠1=60°
∴∠2=60°,
∵AB∥CD
∴∠3=∠1=60°;
(2)①如圖2,過點P作MN∥AB,則∠EPM=∠PEB(兩直線平行,內錯角相等)
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果兩條直線都和第三條直線平行,那么這兩條直線也互相平行)
∴∠MPF=∠PFD(兩直線平行,內錯角相等)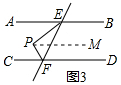
∴∠EPM+∠MPF=∠PEB+∠PFD(等式的性質)
即∠EPF=∠PEB+∠PFD;
故答案為:兩直線平行,內錯角相等;如果兩條直線都和第三條直線平行,那么這兩條直線也互相平行;兩直線平行,內錯角相等;∠EPM+∠MPF;
②過點P作PM∥AB,如圖3所示:
則∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,
即∠EPF+∠PEB+∠PFD=360°,
∴∠PFD=360°-80°-156°=124°;
故答案為:124;
③∠EPF+∠PFD=∠PEB.
故答案為:∠EPF+∠PFD=∠PEB.
點評 本題考查了平行線的判定與性質、三角形的外角性質;熟練掌握平行線的判定與性質,正確作出輔助線是解決問題的關鍵.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | a2•a5=a10 | B. | a2-2ab+b2=(a-b)2 | C. | -(a-b)=b-a | D. | 3a3b2÷a2b2=3a |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
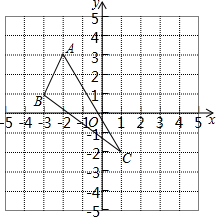 如圖,
如圖,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{x-1}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{16}}$ | D. | $\sqrt{9{a^2}}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com