
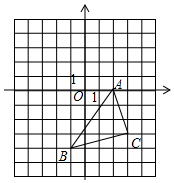
 在如圖所示的直角坐標系中,解答下列問題:
在如圖所示的直角坐標系中,解答下列問題:分析 (1)根據旋轉的性質,可得答案;
(2)根據待定系數法,可得函數解析式.
解答 解:(1)如圖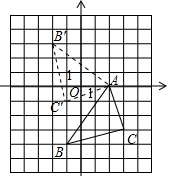 ,
,
(2)設線段B1A1所在直線l的解析式為:y=kx+b(k≠0),
∵B1(-2,3),A1(2,0),
∴$\left\{\begin{array}{l}-2k+b=3\\ 2k+b=0\end{array}\right.$,
∴$k=-\frac{3}{4},b=\frac{3}{2}$,
∴線段B1A1所在直線l的解析式為:$y=-\frac{3}{4}x+\frac{3}{2}$.
點評 本題考查了待定系數法,利用了旋轉的性質得出旋轉后的△A1B1C1,利用待定系數法求B1A1所在直線l的解析式的解題關鍵.


 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
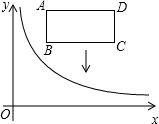 如圖,在平面直角坐標系中,反比例函數y=$\frac{k}{x}$ (x>0)的圖象和矩形ABCD在第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標為(2,6).
如圖,在平面直角坐標系中,反比例函數y=$\frac{k}{x}$ (x>0)的圖象和矩形ABCD在第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標為(2,6).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com