
| A. | (-$\frac{7}{5}$,$\frac{4}{15}$) | B. | ($\frac{7}{5}$,-$\frac{4}{15}$) | C. | (-$\frac{7}{5}$,-$\frac{4}{15}$) | D. | ($\frac{7}{5}$,$\frac{4}{15}$) |
分析 如圖,由圖象可知,B、C、D共線,所以拋物線過A、B、D三點,設拋物線的解析式為y=ax2+bx+c,則有$\left\{\begin{array}{l}{c=3}\\{a+b+c=0}\\{9a+3b+c=4}\end{array}\right.$,求出拋物線的解析式,再求出頂點坐標即可.
解答 解:如圖,由圖象可知,B、C、D共線,
∴拋物線過A、B、D三點,
設拋物線的解析式為y=ax2+bx+c,則有$\left\{\begin{array}{l}{c=3}\\{a+b+c=0}\\{9a+3b+c=4}\end{array}\right.$,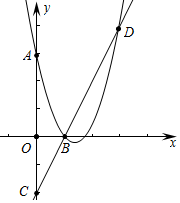
解得$\left\{\begin{array}{l}{a=\frac{5}{3}}\\{b=-\frac{8}{3}}\\{c=3}\end{array}\right.$,
∴拋物線的解析式為y=$\frac{5}{3}$x2-$\frac{8}{3}$x+3=$\frac{5}{3}$(x-$\frac{7}{5}$)2-$\frac{4}{15}$,
∴頂點坐標為($\frac{7}{5}$,-$\frac{4}{15}$).
點評 本題考查二次函數的性質、待定系數法、配方法等知識,解題的關鍵是靈活運用所學知識解決問題,學會用配方法求頂點坐標,屬于基礎題.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:初中數學 來源: 題型:填空題
 甲、乙兩輛汽車分別從A、B兩地同時出發,沿同一條公路相向而行,乙車出發2h后休息,與甲車相遇后,繼續行駛.設甲、乙兩車與B地的距離分別為y甲(km)、y乙(km),甲車行駛的時間為x(h),y甲、y乙與x之間的函數圖象如圖所示,現有4種說法:①甲車的速度是80km/h;②乙車休息了1小時;③兩車相距80km時,甲車行駛了3小時;④乙車兩次行駛的速度相同.上述說法正確的有1個.
甲、乙兩輛汽車分別從A、B兩地同時出發,沿同一條公路相向而行,乙車出發2h后休息,與甲車相遇后,繼續行駛.設甲、乙兩車與B地的距離分別為y甲(km)、y乙(km),甲車行駛的時間為x(h),y甲、y乙與x之間的函數圖象如圖所示,現有4種說法:①甲車的速度是80km/h;②乙車休息了1小時;③兩車相距80km時,甲車行駛了3小時;④乙車兩次行駛的速度相同.上述說法正確的有1個.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m(a+b)=ma+mb | B. | X2+2x+1=x(x+2)+1 | C. | (x+1)(x-1)=x2-1 | D. | x3-x=x(x+1)(x-1) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
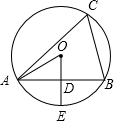 如圖⊙O是△ABC的外接圓,OD⊥AB于點D,交⊙O于點E,∠C=60°,若⊙O的半徑為2,則下列結論錯誤的是( )
如圖⊙O是△ABC的外接圓,OD⊥AB于點D,交⊙O于點E,∠C=60°,若⊙O的半徑為2,則下列結論錯誤的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在Rt△ABC中,∠BAC=90°,∠C=30°,以邊AC上一點O為圓心,OA為半徑作圓,恰好經過邊BC的中點D,并與邊AC相交于另一點F.
如圖,在Rt△ABC中,∠BAC=90°,∠C=30°,以邊AC上一點O為圓心,OA為半徑作圓,恰好經過邊BC的中點D,并與邊AC相交于另一點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com