
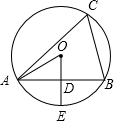
 如圖⊙O是△ABC的外接圓,OD⊥AB于點D,交⊙O于點E,∠C=60°,若⊙O的半徑為2,則下列結論錯誤的是( )
如圖⊙O是△ABC的外接圓,OD⊥AB于點D,交⊙O于點E,∠C=60°,若⊙O的半徑為2,則下列結論錯誤的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
分析 根據由垂徑定理和圓周角定理知,OD是AB的中垂線,有AE=BE,AD=BD,∠AOD=∠BOD=∠C=60°.利用三角函數可求得AD=AOsin60°=$\sqrt{3}$,OD=OAsin∠AOD=OAsin60°=1,AB=2$\sqrt{3}$,從而判斷出選項C是錯誤的.
解答 解:∵OD⊥AB,
∴AE=BE,AD=BD,∠AOD=∠BOD=∠C=60°.
∴AD=AOsin60°=$\sqrt{3}$,OD=OAsin∠AOD=OAsin60°=1.
∴AB=2$\sqrt{3}$.
∴A,B,D均正確,C錯誤.
故選C.
點評 本題利用了垂徑定理和圓周角定理,直角三角形的性質,銳角三角函數的概念求解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | 35+x=2×10 | B. | 35+x=2×(15+10-x) | C. | 35+x=2×(15-x) | D. | 35+x=2×15 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,沿AC方向開山修路,為加快施工進度,要在小山的另一邊同時施工.現在AC上取一點B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直線,那么開挖點E離點D的距離為( )
如圖,沿AC方向開山修路,為加快施工進度,要在小山的另一邊同時施工.現在AC上取一點B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直線,那么開挖點E離點D的距離為( )| A. | 500•sin55° m | B. | 500•cos55° m | C. | 500•tan55° m | D. | $\frac{50}{cos55°}{m}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-$\frac{7}{5}$,$\frac{4}{15}$) | B. | ($\frac{7}{5}$,-$\frac{4}{15}$) | C. | (-$\frac{7}{5}$,-$\frac{4}{15}$) | D. | ($\frac{7}{5}$,$\frac{4}{15}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 13 | B. | 14 | C. | 17 | D. | 13或14 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.
如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com