
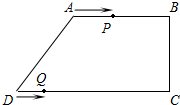
 在四邊形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,點P從點A出發,沿折線A-B-C-D方向以2cm/s的速度勻速運動;點Q從點D出發,沿線段DC方向以1cm/s的速度勻速運動,已知兩點同時出發,當一個點到達終點時,另一點也停止運動,設運動時間為t(s).
在四邊形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,點P從點A出發,沿折線A-B-C-D方向以2cm/s的速度勻速運動;點Q從點D出發,沿線段DC方向以1cm/s的速度勻速運動,已知兩點同時出發,當一個點到達終點時,另一點也停止運動,設運動時間為t(s).分析 (1)過A點作AM⊥CD于M,根據勾股定理可求得DM=6,進而求得DC=16;
(2)當∠PQC=45°時,需要分類討論:①當點P在線段AB上,②當點P在線段BC上,通過作輔助線構建等腰直角三角形,利用等腰直角三角形的性質列出方程,由方程的解即可得到答案;
(3)分三種情況討論:①當點P在線段AB上,②當點P在線段BC上,③當點P在線段CD上,根據三種情況點的位置,即可求得t的值.
解答  解:(1)如圖1,過A點作AM⊥CD于M,則四邊形AMCB是矩形,
解:(1)如圖1,過A點作AM⊥CD于M,則四邊形AMCB是矩形,
∴AM=BC=8,MC=AB=10,
∵AD=10,
∴DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴CD=DM+CM=6+10=16;
(2)①當∠PQC=45°時,點P在AB上,點Q在DC上,如圖2,
此時PT=QT.
過點P作PT⊥CD于點T,則QT=PT.
由題意得:BP=CT=10-2t,
則QT=16-t-(10-2t)=6+t,PT=8,
∴6+t=8,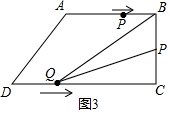
∴t=2;
②當∠PQC=45°時,點P在AB上,點Q在DC上,如圖3,
此時PC=18-2t,QC=16-t.
由PC=QC得到:18-2t=16-t,
解得t=2(不合題意,舍去)
綜上所述,當t=2時,∠PQC=45°;
(3)①當點P在線段AB上時,即0≤t≤5時,如圖4,
S△BPQ=$\frac{1}{2}$BP•BC=$\frac{1}{2}$(10-2t)×8=10,
解得t=3.25;
②當點P在線段BC上時,即5<t≤9時,如圖3,
BP=2t-10,CQ=16-t,
∴S△BPQ=$\frac{1}{2}$BP•CQ=$\frac{1}{2}$(2t-10)×(16-t)=10,
化簡得:t2-21t+90=0,
解得 t1=15(舍去),t2=6;
③當點P在線段CD上時,
若點P在Q的右側,即9≤t≤$\frac{34}{3}$時,則有PQ=34-3t,
S△BPQ=$\frac{1}{2}$(34-3t)×8=10,
解得t=$\frac{63}{6}$,
若點P在Q的左側,即$\frac{34}{3}$<t≤16時,則有PQ=3t-34,
S△BPQ=$\frac{1}{2}$(3t-34)×8=10,
解得t=$\frac{73}{6}$;
綜上,滿足條件的t的值存在,分別為3.25或6或$\frac{63}{6}$或$\frac{73}{6}$.
點評 本題是四邊形的綜合題,考查了矩形的判定和性質,平行四邊形的性質,勾股定理的應用以及三角形的面積等,分類討論的思想是本題的關鍵.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2+2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com