
分析 如圖,設△AOD的面積為x,則△ODC的面積為4-x.由AD∥BC,推出△AOD∽△COB,可得$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AO}{OC}$)2,因為$\frac{{S}_{△AOD}}{{S}_{△ODC}}$=$\frac{OA}{OC}$,得到$\frac{x}{9}$=($\frac{x}{4-x}$)2,解方程即可.
解答 解:如圖,設△AOD的面積為x,則△ODC的面積為4-x.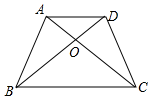
∵AD∥BC,
∴△AOD∽△COB,
∴$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AO}{OC}$)2,
∵$\frac{{S}_{△AOD}}{{S}_{△ODC}}$=$\frac{OA}{OC}$,
∴$\frac{x}{9}$=($\frac{x}{4-x}$)2,
解得x=1或16(舍棄),
∵S△ABD=S△ADC=1,
∴S△AOB=S△DOC=3,
∴梯形ABCD的面積=1+3+3+9=16,
故答案為16.
點評 本題考查相似三角形的判定和性質、梯形的性質等知識,解題的關鍵是熟練掌握相似三角形的性質,學會用方程的思想思考問題,屬于中考常考題型.


科目:初中數學 來源: 題型:填空題
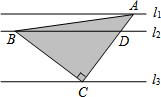 如圖,直線l1∥l2∥l3,且l1與l2的距離為1,l2與l3的距離為3.把一塊含有45°角的直角三角板如圖放置,頂點A、B、C恰好分別落在三條直線上,則△ABC的面積為$\frac{25}{2}$.
如圖,直線l1∥l2∥l3,且l1與l2的距離為1,l2與l3的距離為3.把一塊含有45°角的直角三角板如圖放置,頂點A、B、C恰好分別落在三條直線上,則△ABC的面積為$\frac{25}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
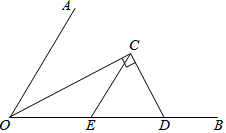 如圖,∠AOB=60°,OC平分∠AOB,C為角平分線上一點,過點C作CD⊥OC,垂足為C,交OB于點D,CE∥OA交OB于點E.
如圖,∠AOB=60°,OC平分∠AOB,C為角平分線上一點,過點C作CD⊥OC,垂足為C,交OB于點D,CE∥OA交OB于點E.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.$\stackrel{•}{3}$$\stackrel{•}{4}$ | B. | $\frac{22}{7}$ | C. | $\sqrt{16}$ | D. | 0.020020002… |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
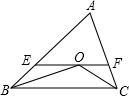 △ABC中,∠ABC、∠ACB的平分線相交于點O,過點O作EF∥BC分別交AB、AC于E、F.
△ABC中,∠ABC、∠ACB的平分線相交于點O,過點O作EF∥BC分別交AB、AC于E、F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將一個長為10cm,寬為8cm的矩形紙片從下向上,從左到右對折兩次后,沿所得矩形兩鄰邊中點的連線(虛線)剪下,再打開,得到的四邊形的面積為( )
如圖,將一個長為10cm,寬為8cm的矩形紙片從下向上,從左到右對折兩次后,沿所得矩形兩鄰邊中點的連線(虛線)剪下,再打開,得到的四邊形的面積為( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com