
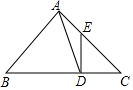
 在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.
在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.分析 (1)由BD=AB,得∠BAD=∠BDA,又因為∠BAC=90°,DE⊥BC,根據等角的余角相等,得∠EAD=∠ADE,從而問題得證;(2)由∠BAC=90°,DE⊥BC,∠B=45°,可得等腰三角形ABC、DEC,由 BD=AB,可得等腰三角形ABD.
解答 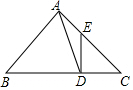 解:(1)證明:∵BD=AB,
解:(1)證明:∵BD=AB,
∴∠BAD=∠BDA
∵DE⊥BC,
∴∠BDE=90°
又∠BAC=90°,
∴∠EAD=∠EDA.
∴AE=DE,
即△ADE是等腰三角形.
(2)還有三個等腰三角形,△ABD、△ABC、△CDE.
點評 本題考查了等腰三角形的性質和判定及互余的性質.判斷等腰三角形的辦法:(1)根據定義,有兩條邊相等的三角形是等腰三角形;(2)根據性質,等角對等邊.


科目:初中數學 來源: 題型:解答題
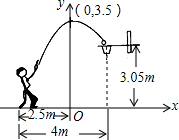 宜昌四中男子籃球隊在2016全區籃球比賽中蟬聯冠軍,讓全校師生倍受鼓舞.在一次與第25中學的比賽中,運動員小濤在距籃下4米處跳起投籃,如圖所示,球運行的路線是拋物線,當球運行的水平距離為2.5米時,達到最大高度3.5米,然后準確落入籃圈.已知籃圈中心到地面的距離為3.05米.
宜昌四中男子籃球隊在2016全區籃球比賽中蟬聯冠軍,讓全校師生倍受鼓舞.在一次與第25中學的比賽中,運動員小濤在距籃下4米處跳起投籃,如圖所示,球運行的路線是拋物線,當球運行的水平距離為2.5米時,達到最大高度3.5米,然后準確落入籃圈.已知籃圈中心到地面的距離為3.05米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 10,24,26 | B. | 15,20,25 | C. | 8,10,12 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
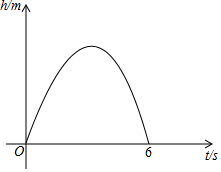 從地面豎直向上拋出一小球,小球的高度h(單位:m)與小球的運動時間t(單位:s)之間的關系式是h=30t-5t2(0≤t≤6).
從地面豎直向上拋出一小球,小球的高度h(單位:m)與小球的運動時間t(單位:s)之間的關系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
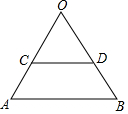 如圖,△ABO是正三角形,CD∥AB,把△ABO繞△OCD的內心P旋轉180°得到△EFG
如圖,△ABO是正三角形,CD∥AB,把△ABO繞△OCD的內心P旋轉180°得到△EFG查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com