
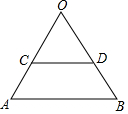
 如圖,△ABO是正三角形,CD∥AB,把△ABO繞△OCD的內心P旋轉180°得到△EFG
如圖,△ABO是正三角形,CD∥AB,把△ABO繞△OCD的內心P旋轉180°得到△EFG分析 (1)畫出△ABC的中線的交點即為點P再把△ABO繞△OCD的內心P旋轉180°得到△EFG即可.
(2)想辦法求出AP的長即可利用圓周長公式解決問題.
解答 解:(1)點P和△EFG如圖所示.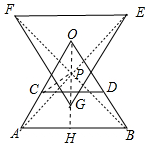
(2)延長OP交CD于G,交AB于H,
∵OA=3$\sqrt{3}$,CD=2$\sqrt{3}$,
∴OP=2,OH=$\frac{9}{2}$,
∴PH=OH-OP=$\frac{5}{2}$,AH=HB=$\frac{3\sqrt{3}}{2}$,
∴AP=$\sqrt{P{H}^{2}+A{H}^{2}}$=$\sqrt{(\frac{5}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$=$\sqrt{13}$,
∴A點運動到E點路徑的長=$\frac{1}{2}$•2π•$\sqrt{13}$=$\sqrt{13}$π.
點評 本題考查作圖-基本作圖、等邊三角形的性質、三角形的內心、軌跡等知識,解題的關鍵是靈活運用所學知識解決問題,記住圓的周長公式,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
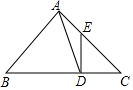 在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.
在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com